June 15, 2020 by mrssteven

“I’ll retire to Bedlam”

Our school year has ended. Nobody is going to deny the unusual circumstances that we were all thrown into during the last ten weeks of our school year! In fact I can never remember a single situation affecting schooling worldwide like this pandemic has! Teachers and students the world over scrambled for weeks trying to see if any teaching style could match the face to face teaching/learning we are all so used to. But that burden is done for my school district. Our school year is over. Our rooms are ready for summer cleaning, and our fifth grade students are ready to move on to the middle school in the fall. In the midst of what has not at all felt normal, those simple acts of getting our rooms ready for cleaning and our students ready for the next grade have brought us back to the routine we expect at this time of year.

But there has been one more big change in my building. Six of my colleagues have retired. SIX! If you work in a large district, that probably seems like a pittance. You probably lose many more than that to retirement each year. But in my world, we don’t. I have worked in the same district and at the same grade level for 26 years. I know each of the six retirees personally. One of them I knew as a parent when both of our children were in second grade together. Another of them was our children’s second grade teacher. One is married to a former pastor of my church down the street from our school. One has been my 5th grade colleague for all of my 26 years. Only two of the six began working at our school after me. So you can see just how unique this retirement situation is, and how odd it will feel to begin a new school year without the personalities that have brought joy and camaraderie for so many years.

I often speak of the staff at our school as one of our strongest assets, and because these six people have been so special, I spent a lot of time thinking of what their retirement means to me. And then (if you know me at all, you know where this is going), I began to wonder what the word ‘retirement’ means to anyone. What is its story? As a kid I used to think it meant that someone was tired of doing their job, so they stopped doing it. Is it really as simple as that?

Starting at Etymonline with the word ‘retire,’ I found that this word was first attested in the 1530’s. At that time it was something armies did. It meant “to retreat.” It was borrowed from the earlier Middle French word retirer “to withdraw.” The <re-> had a sense of “back” and the <tirer> had a sense of “draw.” Looking at the Oxford English Dictionary, We get a better idea of how this word was used in French.

Middle French, French retirer to pull or draw (something) back (12th cent. in Old French),
to remove, withdraw (something from someone) (13th cent.),
to remove (someone from a particular place or position),
to free (someone from captivity),
to keep (something) in reserve,
to deter or turn (someone) aside (from a vice, etc.) (all 15th cent.),
also (reflexive) to withdraw, go away (end of the 14th cent.),
to go off to somewhere peaceful or secluded,
to withdraw somewhere for protection,
(in military context) to retreat (all 15th cent.),
(reflexive, of the sea) to ebb (c1500),
(reflexive with de ) to give up (a habit, etc.) (1508),
(reflexive with de ) to cease to perform or pursue (a specified activity, mode of employment, post, etc.) (1538),
(reflexive with de ) to cease to frequent (someone) (1553)

The OED goes on to say, “French retirer shows a number of senses not paralleled in English, especially senses related to the core meanings ‘to take back, take away, remove’. In modern French the meanings ‘to leave employment’ and ‘to withdraw (something) from service’ are usually expressed by constructions with retraite (retreat), rather than with retirer.” Isn’t that last bit interesting? What we in English speaking countries refer to as retiring, the French refer to as retreating. What is extra interesting is that both of those words come to us from French!

Checking with my Chambers Dictionary of Etymology, I find that ‘retreat’ is first attested (in English) in about 1300 and was a signal for a military withdrawal. It was borrowed from Old French retret, retrait, and is from Latin retrahere “draw back.” Since it can be traced back to Latin, it is an older word than ‘retire.’ As I mentioned above, ‘retire’ was first attested in the 1530’s.

Heading back into Etymonline, I find that it wasn’t until the 1640’s that this word was applied to a person withdrawing from an occupation. Interesting. Retiring from a job simply meant to withdraw from that job. The sense and meaning hasn’t changed! But it has broadened. By the 1660’s, it was also used to mean “to leave company and go to bed.” Every once in a while I come across this use in a story. Perhaps you have too. Someone might say, “I’m feeling tired. I’m going to retire for the night.” As we’ve found out earlier, as this word was associated with the military, it meant “withdraw, lead back,” but by the 1680’s it also meant “to remove from active service”. That is a very similar sense to retire from one’s occupation, isn’t it? The final sense listed at Etymonline is from 1874, and it is the baseball sense of “to put out.” So to retire the runner, could mean you threw the runner out at the base.

Two words that I found while making this matrix fascinated me. The first is ‘retiracy.’ I’ve never heard of it that I can remember. Etymonline describes it as modeled on ‘piracy’ in 1824 American English. Sounds like humans playing around with their language again! I can’t wait to wish my friends fun in their retiracy!

The second fascinating word on this matrix, and the only word here that does not have anything to do with leaving a job, is ‘tirade.’ When I think of a tirade, I think of a long, often angry speech, or perhaps two people bickering back and forth. The interaction is drawn out, hence the base <tire>!

Have you noticed that so far there’s been no mention of being fatigued, exhausted, or tired? So if the base of ‘retire’ does not have the same base we see in ‘tired,’ then what’s the story of <tired>?

credit to marfis 75 on flicker

Combining what I found in Chambers and at Etymonline, I read that before 1460, this word was spelled tyren. It was developed from Old English tēorian at about 1000 and in Kentish tiorian before 800. It was used to mean “to fail, cease; become weary; make weary, exhaust.” The fact that the <tire> in ‘retirement’ and the <tire> in ‘tiresome’ come from completely different languages gives us evidence that they are not related etymologically, and most certainly won’t be related morphologically. They are two completely different words!

Even though most people wouldn’t consider the kind of tire we see on our cars to be confused with either of these other bases, I’d still like to address it. After all, it is another base that has this same spelling of <tire>. If you’ve never looked up this word, you are in for a treat!

Tire - Wikipedia

This word dates back to 1485 and was used to mean a band around a wheel. At that time it was spelled <tyre> and meant the iron rim of a carriage wheel. What’s fascinating is that it is a shortened form of the word ‘attire.’ The prefix is an assimilated form of <ad-> “to” and the base is <tire> “equipment, dress, covering.” According to Etymonline, “The notion is of the tire as the dressing of the wheel.” My Chambers Dictionary gives further information indicating that the band of rubber on the rim of the wheel was first recorded in 1877. It was first used on bicycles before being used on cars. I’m sure the iron lengthened the life of a carriage wheel before then, but I can’t imagine what kind of a bumpy ride it provided! And it’s obvious that improvements have been made on the rubber tire ever since! Another fascinating thing about this word is its spelling. When it first appeared, it was spelled <tyre>. From the 1600’s through the 1700’s, the standard spelling was <tire>. But then at the beginning of the 1800’s, the British revived the spelling of <tyre> which still remains standard in Britain while in the United States, the spelling remains <tire>.

While we’re on the subject of tires (as in the covering on a wheel) I found an interesting bit on the word ‘tire-iron.’ Originally this was one of the iron plates off of the older fashioned wheels and was used to pry the tire off the wheel. The name ‘tire-iron’ caught on in 1909. We still call the tool we use to pry a wheel off of the rim a tire-iron, and now you know why.

Before I retire this topic …

Did you recognize the title of this post? It is a line from A Christmas Carol by Charles Dickens. In the passage, he has just had an exchange with his nephew and is reflecting on how silly it is to celebrate Christmas when you haven’t any money. It is the last line in the following excerpt:

“There’s another fellow,” muttered Scrooge, who overheard him: “my clerk, with fifteen shillings a week, and a wife and family, talking about a merry Christmas. I’ll retire to Bedlam.”

So now that you know more about the word ‘retire,’ you can understand that Scrooge means to withdraw from this conversation and head straight for the insane asylum in London, (St. Mary of Bethlehem Hospital, which was commonly referred to as Bedlam at the time). He can’t understand how people with very little money can be so full of joy, while he who has more than he needs, is miserable. He sees this disconnect as him being surrounded by insanity. His pursuit of wealth doesn’t just cloud his thinking, it blocks him from pursuing human relationships, where real happiness lies. I find it remarkable that a look at a word I kind of had a sense about, in a passage I’ve heard many times, suddenly creates a sharper focus on the meaning of that word. In turn, the deeper understanding of the word shines a brighter light on the overall meaning of the passage, as if being viewed from a wider lens.

Perhaps people associated retired with having something to do with being weary or fatigued, because generally the people who choose to retire are older. As of November 2019, the most common age for retirement in the U.S. was 62. Those people have worked at their jobs for many years and it is not a stretch to imagine they might be tired of it or tired because of it. And that may certainly be the case for some. But if we look at the words and understand what they mean, we can better understand how to use them! We can get an orthographical kick out of the fact that we have three bases, all spelled exactly the same (<tire>), but deriving from three different ancestors and with three distinct meanings! Some of those who are beginning to see the value in teaching children about morphology are still wagging about teaching them etymology. Yet here’s evidence that etymology can hold the key to an understanding that neither morphology nor pronunciation can provide on their own. That’s why we must teach students to look at all three.

As a farewell to my colleagues I wrote up a shortened form of this post and gave it to each. I closed with a quote from the Century Dictionary that I particularly love.

“Retirement is comparative solitude, produced by retiring, voluntarily or otherwise, from contact which one has had with others.”

I think of my colleagues, my friends, as withdrawing from employment at our school and enjoying comparative solitude. They will leave the “noise” of education behind and take with them every laugh between friends, every tender moment, and every triumphant teaching joy. They will immerse themselves in comparative solitude. I couldn’t wish for anything better than that! Congratulations, my dear friends!

March 22, 2020 by mrssteven

When You Have a Febriferous Illness, You Need a Febrifuge!

Ricard Canals (1876 – 1931) Sick Child (Octavi, the artist’s son) c1903

I received a scary call a few weeks ago from my daughter. My 3 year old granddaughter had just had a seizure and her dad was with her, at home, waiting for the ambulance. My daughter, who had called from her car, was on her way home from work and had just picked up her younger daughter from daycare when she received the call from her husband. He had stayed home with June, who was sick with the fever and yucky feelings that had been going around her preschool.

We were all so scared. I was immediately picturing my granddaughter and what was happening to her. Was she scared? How out-of-it was she? How long did it last? But then I thought of her parents and how scared they must have been. It pulled at my heart to know all any of us could do was wait and see now. I am still my daughter’s mom and number one worrywart of her emotional and physical well-being. I have also grown to see what a truly wonderful husband and dad my son-in-law is, and I knew this had no doubt scared the liver out of him.

I’ll keep you in suspense no longer. After five hours at the hospital, and after having ruled out that the seizure was caused by a Urinary Tract Infection or by the small skin infection she had on her finger, it was decided that she had a febrile seizure. A febrile seizure is one caused by fever. Children can have febrile seizures if their fever spikes unexpectedly and if this kind of seizure is present in the family history. It turns out that this happened to their nephew as well. They usually don’t happen after the age of 6, but because she’s had one now, she is more likely than other children to have another. It was certainly scary! Moving forward, we will all watch for signs of fever with vigilant eyes.

It wasn’t until a few days later and everything was calm again that I could think more about that word <febrile>, and wonder if it was related to February. You see what happens once that dark cloak of “memorize the dictionary definition and you’ll be fine” has been lifted? So many words catch my attention now. This one was less common and therefore caught my attention right away.

According to the Chambers Dictionary of Etymology, febrile is an adjective “of fever, feverish” first attested in 1651. It was either borrowed through French fébrile, or directly from Medieval Latin febrilis. Earlier it was from Latin febris “a fever.”

At the Oxford English Dictionary I found this sentence from 1483, “Al that yere she was seke and laboured in the febrys.” There were also the spellings febres from 1527 and febris from 1535. Besides these Middle English spellings, I found other relatives. I put them in chronological order according to their date of attestation. The words with the asterisk are obsolete, although many of the others (as you may guess) are rarely used.

febrous – adj., as early as 1425, “affected with fever.”
*febris – n., 1483, “a fever.”
febricitant – n., adj., ?1541, “affected with fever.”
*febricitation – n., 1598, “the state of being in a fever.”
febrile – adj., 1651, “feverish.”
*febrient – adj., 1651, “feverish.”
*febricitate – v., 1656, “to be ill of a fever.”
*febriculous – adj., 1656, “slightly feverish.”
febrifugal – adj., 1663, “adapted to subdue fever.”
*febrifugous – adj., 1683, “adapted to subdue fever.”
febrifuge – adj., n., 1686, “a medicine to reduce fever.”
febrific – adj., 1710, “producing fever.”
febriculose – adj., 1727, ” slight fever.” Also febriculosity.
febricula – n., 1746, “fever of short duration.”
febrifacient – adj., n. 1803, “fever producing.”
febricity – n., 1873, “the state of having a fever.”
febriferous – adj., 1874, “producing fever.”
febricule – n., 1887, Anglicized form of febricula “slightly feverish.”

Isn’t it something to see the variety of spellings/uses for this word over 400 years? As you read through the list, do you recognize the suffixes that signal nouns and adjectives? I’m fascinated that in that entire list there is only one form used as a verb. <febricitate>. Do you notice the <ate> suffix there? It was used as a noun first, <febricitation>. This <ate> suffix signaling a verb but then changing the function of the word to a noun by the addition of an <ion> noun, is something I always look at with my students. In the following list, the verb form is first and the noun form is second.

precipitate, precipitation
illuminate, illumination
infiltrate, infiltration
hydrate, hydration
illustrate, illustration

Once I get them started, they continue the list on their own. Once they see this for themselves, and they know the suffixing convention of replacing the single final non-syllabic <e> on an element when adding a vowel suffix, they don’t believe people who tell them that *<tion> is a suffix. I don’t have to convince them of that fact. The evidence that they have collected convinces them.

There’s just so much to notice about this list! As I was putting it together and announcing the words to myself, I have to say that <febriferous> was my favorite. I laughed at myself trying to say it even two times in a row! Perhaps you’ll have better luck?

Other relatives that stick out to me are febrifuge, febrifugal, and febrifugous. You’ve probably noticed the second base there, <fuge> from Latin fugare “cause to flee, put to flight, drive off, chase away.” A febrifuge is a medicine that will drive off the fever. I love imagining my little June’s fever being driven off by little medicine superheroes!

Interestingly enough, I came across the word <feverfew> which is from Old English feferfuge. (Do you notice what I noticed? – that that second <f> in the Old English spelling is the unvoiced version of <v>?) Earlier it was from Late Latin febrifugia, from Latin febris “fever” and fugare “put to flight.” According to Etymonline, this modern English word is probably a borrowing from Anglo-French. According to information at Wikipedia, feverfew was used as a traditional herbal medicine, but is no longer considered useful for reducing a fever.

Feverfew (Tanacetum parthenium)
By Vsion (2005). Photo via Wikipedia public domain.

Getting back to the word <febrifuge> and the second base in that word <fuge>, I pondered that sense and meaning of “cause to flee, drive off, chase away,” and it made sense to me that this must be the same <fuge> that I see in <fugitive>. So I went to Etymonline and looked at <fugitive> to make sure that they shared the same ancestor. This is what I found:

Although this seems to be a match, I noticed something about both the spelling of the Latin verb this word is from and the denotation of that verb. This word derives from Latin fugere “to flee, fly, take flight, run away, go into exile,” whereas the <fuge> in <febrifuge> comes from Latin fugare “cause to flee, drive off, chase away.” Do you see the difference in spelling of the Latin verb for each? They each have a different infinitive suffix. That means they are two separate Latin verbs! Then I looked closely at the denotation of each and realized that the Latin verb fugare has a sense of chase away something and the Latin verb fugere is the thing that has been chased away or has taken flight! I wanted to find out related words for each so I went back to Etymonline.

First I typed fugare into the search bar. That way I would probably find words whose ancestor is the Latin verb fugare. I found only three entries: feverfew, -fuge, and febrifuge. I found something very interesting in the -fuge entry.

Look at the line following the bolded <febrifuge>. It says, “but form from Latin fugere.” I interpret that to mean that Latin fugere existed in words earlier than Latin fugare. I took a quick look at <fugitive> in the OED and sure enough, the word is attested in 1382, which is earlier than <febrifugal> which was attested in 1663!

It was time to look at Lewis & Short. The infinitive form of the Latin verb is the second one out of the four.

fŭgo, fŭgare, fugāvi, fugātum
“to put to flight, drive or chase away”

fŭgĭo, fŭgere, fŭgi, fŭgĭtum
“run away”

Yep! Two separate verbs with two separate yet related denotations. One has become more productive than the other, hasn’t it?

#####
There is a very thought provoking comment at the end of the post that I encourage you to look at. It is written by someone who has studied Latin at a deeper level than I have. She has been collecting Latin verbs, including the two I have pointed to above. I am thinking carefully about what she has said, and I encourage you to do the same. I know there is no rush in scholarship, so I’m not concerned that I don’t completely embrace yet what she is pointing out. I have questions to pose before then. This is the way scholarly learning works. I don’t take anyone’s word for anything. I need to understand things for myself. I appreciate things being shown to me, but unless they make sense to me, I must keep questioning.
#####

Now that I’ve followed that interesting path, I’d like to get back to my original question. Is <febrile> related to <February>? I bet that at this point you’re guessing that it is not. If it was, wouldn’t it have shown up as a related word in the OED? So if it isn’t related to “fever”, what is it related to?

Looking further at the Chambers Dictionary of Etymology, I can add to that that this idea of purification refers to the Roman feast of purification held in February, which at that time was the last month of the ancient Roman calendar. It was after 450 BC that it became the second month and was called solmonath by the Old English which meant mud month.

The base <febr> “fever” may have had many related words a few hundred years ago, but not that many of them are still in use today. The word that we commonly use is <fever>. Does that mean it’s a newer word? Interestingly enough, it’s not. According to Chambers, it developed from Old English (c1000) fēfer, fēfor. It was borrowed from Latin febris “fever” and is related to fovēre “to warm, heat.” Later on in Middle English (1393) it is spelled fievre where it was borrowed from Old French fievre, which was from Latin febris.

This word also has a lot of related words that have become obsolete.
We no longer use:

feverly – adj., 1500, “relating to fever.”
feverable – adj., 1568, “characterized by having a fever.”
feverite – n., 1800, “a person ill with fever.”

On the other hand, many related words I found at the OED are still very much in use today:

fever – n., 1000, “abnormally high body temperature.”
fever – v., early OE, “affected with abnormally high body temperature.”
fevery – adj., OE, “affected by fever, perhaps causing fever.”
fevering – adj., ?1200, “becoming feverish.”
feverous – adj., 1393, characteristic of having a fever.”
feverish – adj., 1398, “relating to fever.”
fevering – n., 1450, “a feverish state.”
fevered – adj., 1605, “showing symptoms associated with a high temperature.”
feverishness – n., 1638, “the condition of having a fever.”
feverishly – adv., 1640, “in a manner relating to a fever.”
feverless – adj., 1662, “without a fever.”
fever tree – n., 1727, “bark of certain trees used to treat fevers.”

Take a look for a moment at the above list and notice how many of those words you have used. Then notice how old those words are. Words amaze me every day. There is so much to know and so many connections to make! I can’t help but wonder about these two bases, <febr> and <fever>. They both share the Latin root febris and the same denotation, yet the one is much more recognizable than the other. The <febr> base is still around, but probably more well known in the medical field. The sciences are full of words with roots in either Greek or Latin. The <fever> base is still very much around also, and known well by the common people — by the ancestors of the common people who spoke the Old English language.

One of my very favorite things to discover are bases that look the same but aren’t. Today I found two! I wouldn’t have done so without the help of excellent reference materials, and without having been taught how to use those materials. I am grateful that for now my granddaughter is feverless, but like I said earlier, her parents are vigilant. Should she get a febriferous illness again, they are ready with a febrifuge.

Below is a picture of Cinchona pubescens. This is an example of a fever tree. According to Wikipedia, the bark of several species of this flowering plant yields quinine which was an effective treatment for the fevers associated with malaria up until 1944.

File:Cinchona.pubescens01.jpg

Credits : US Geological Survey – Photo by Forest & Kim Starr

January 1, 2020 by mrssteven

Waiting for the Tides to Change

Picture courtesy of www.willstevenphotography.com

When you begin to learn what is real about English spelling, you also begin to swim against the current in an educational world that has been led to believe that reading is simply the act of unlocking a code – that code being the letters of our alphabet. In many such programs, teaching reading means beginning with isolated spoken sounds and matching them to written letters. That is followed by practice at “sounding it out.” The newest buzz word for this is “orthographic mapping.” The student is taught to attach a pronunciation to groups of 1-4 letters. These letter groupings are somewhat consistent, but there are a lot of them to know to automaticity in order for a child to read fluently. If “sounding out” a word can’t make it recognizable, it is deemed “irregular.”

Those in the front lines (tutors, interventionists, and teachers of pre-k, kindergarten, 1st grade, and 2nd grade) who have received intense training in these phonics-first models or have grown up in a system using these models, seem to struggle the most in imagining a world that begins with meaning and then considers morphology, etymology, and phonology as interrelated in explaining a word’s spelling. Interrelated. Not one first in isolation, but the three facets of a word coming together to explain its meaning, spelling, and pronunciation. In this way the student is presented with a system right from the start. They are not taught specific strategies for reading that are then misapplied to writing. They are not taught that English spelling is crazy or that it cannot be understood. Instead the students learn from the start how speaking, reading, and writing can be used to represent our thinking. Much of the system we have is logical and predictable. (Many of the suffixing and other conventions are predictable. Learning that words are built from bases and that the spelling of bases within a morphological family is consistent is logical.) Students learn how to question what they do not understand. In fact their questions are encouraged and even celebrated, sending the underlying message that asking questions is key to learning. They are taught to see meaning relationships between words that share a base element, and that even when the pronunciation within that word family shifts, the spelling doesn’t. They are taught that all words have a structure, a spelling, and a pronunciation that can be explained and understood.

When first hearing about Structured Word Inquiry, many trained educators who have experienced the gamut of “spelling programs extraordinaire” figure this too is full of promises it can’t fulfill. And when they hear there is no scope and sequence, they get downright jittery. How in the world will they know what to say and what to teach without a teacher guide to tell them? But that’s just it. Structured Word Inquiry is NOT A PROGRAM. It is a course of investigation driven by curiosity. Rather than a list of words to learn each week, there are principles to visit and revisit via words chosen that enhance curricular content, are someone’s personal favorites, or are suggested for any of a number of reasons. There is no teacher manual full of answers because an answer to every question is not what I want my students to expect.

Ponder that for a moment.

There is no teacher manual full of answers because an answer to every question is not what I want my students to expect.

In the education world, when a question is posed, everyone searches for an answer. They stop when they get one they are satisfied with, and the conversation moves on. But, especially in the sciences, don’t we accept that answers are temporary? That at some future time, some scientist may discover a different answer to the same question? A deeper understanding? THAT is the same mindset I use when teaching Structured Word Inquiry. Sometimes I refer to it as Scientific Word Investigation, which more appropriately represents the scientific rigor and evidence-based thinking that is integral to this.

Unfortunately, we live in an educational world in which most people have stopped wondering about a word’s spelling and have just fully accepted that our language has no rhyme or reason to it. The teachers think they are teaching how our spelling system works, but if they are really really honest with themselves, they will admit that they wish they could explain the spelling of words like of, come, have, does, they, laugh, give, the, and countless others that end up on Word Walls in far too many classrooms. Every year a child is in school, they encounter more and more of these words that the adults only know to shrug their shoulders at, reinforcing the idea that English spelling is crazy. It is amazing to me that we all accept (and yes, I accepted it too for many years) the idea that there is no explanation to be had for words that can’t be sounded out.

But why is it like this? Why aren’t the explanations accessible to teachers? Why have teachers been told instead to use “rules” that don’t statistically work? Not only am I referring to the old “I before E” rule, but also to the “Two Vowels Go Walking” rule. Did you know that the “i before e” part of that rule is only accurate 75% of the time? Or that the “except after c” part of that rule is only accurate 25% of the time? Or that when looking at the top (meaning most common) 2,000 words, the “when two vowels go walking” rule was found to be accurate only 36% of the time?

Here are two more “rules” that deserve to be banned. The first says, “When a stressed syllable ends in e, the long sound of the vowel is used, and the final e is silent.” It works for words like bike, pope, and rake, and doesn’t work for give, love, and move. Teachers will find it surprising that it is accurate only 68% of the time. (Those teaching with SWI will recognize a different way to explain what is happening there – it has to do with the function of the single final non-syllabic <e>.) The second rule says, “When there is only one vowel in a stressed syllable and the vowel is followed by a consonant, the short vowel sound is used.” This works for fix, hop, and cat, but not for mind, wild, and fold. This one too works only 68% of the time.

I find it astounding that creative people have used their talents to come up with these “rules” instead of demanding to understand why words are spelled the way they are! Is it really that there is no explanation? Hardly. Are the explanations really so complicated that teachers and children alike can’t learn or understand them? Again, hardly.

In my opinion, the three biggest problems are these:

ONE

The inaccuracies have been embedded in the teaching for so long that as a society we have become complacent. There is a general acceptance of the notion that English spelling is crazy and can’t be understood. We see this all over the internet. People print what they perceive to be the ridiculousness of English spelling on coffee cups and T-shirts, and everybody laughs. People offer proof of the craziness of English spelling by asking why ‘bomb’ doesn’t rhyme with ‘tomb’ or ‘comb’. But who said they had to? You can blame that expectation on teachers who first taught those people to read. They may not have said it specifically, but after having students complete worksheet after worksheet with cat, rat, sat, pat, tip, sip, rip, lip, and cup, sup, pup, children get the message. Words that have the same letter string will always rhyme. And no one ever tells them differently. Children learn what you tell them, but also what you imply.

TWO

Teachers cannot teach what it is that they themselves do not understand. This lack of understanding is so pervasive because there are very few colleges that equip teachers with orthographic understanding. The textbooks offered to future teachers of reading are smattered with the inaccurate rules listed above. It would be difficult indeed to sort out what is worth using with children and what is not. And the curricular materials school districts spend millions on every year are no different. Many teachers can sense that the materials are not helping their students, but don’t know enough on their own to understand specifically what parts are utter nonsense. All the company has to do is slap the words “evidence based” or “research based” on the cover, and the school districts are all in. No one in any of those districts is reading any of that “evidence” or “research” and the company counts on that. The companies simply put a new spin on the old content and market it. School districts see where there are weaknesses in their ELA scores, and want to find something that will help their teachers improve scores and ultimately assist their students in becoming better at reading and writing. They believe the companies know what they are doing. But those administrators, like the teachers, like the teacher-prep colleges, and like the curricular material companies don’t understand English spelling themselves. The curriculum companies get as creative as they can in presenting spelling as a fun activity, but the bottom line is that one cannot teach what one doesn’t understand.

THREE

Many children will learn to read even without understanding how our spelling system works. This is what keeps so many spelling programs and curricular materials in business. It is also what keeps so many well meaning teachers and their students in the dark. If a child can read, then what does it matter whether or not they understand a word’s spelling? There will always be spellcheck, right? This idea that reading is primarily about sounds represented as letters may seem to be so obvious when a child is learning to read. But as they advance through the grades and encounter longer and more interesting words, their missing understanding about the morphology and the etymology that affects the phonology is the thing that becomes obvious. Why don’t they know that some letters are etymological or orthographic markers, or that a word’s etymology has much to do with the graphemes that spell it? Why weren’t they taught that English spelling is a system and that each year their understanding of that system could grow to accommodate any newly acquired words? Instead it is assumed that if they learn to read in kindergarten and 1st grade, they will naturally maintain that reading proficiency and spelling proficiency automatically as they move through grades, even when the materials used include inaccurate information such as I’ve mentioned above.

An example of such nonsense was recently brought to my attention by a teacher using Words Their Way. Her students were asked to spot the <un> in unplanned, unprepared, unlock and uncle. Really? The <un> in three of those words is obviously a prefix. Why would ‘uncle’ be included here? Are the students supposed to think it also has an <un> prefix, or is this just an indicator that children are not being taught that a word has structure (is comprised of morphemes)? Then, within that same week, the same teacher told me about the task in which her students were supposed to spot the <re> in rethink, replay, reheat and reptile. She wondered what she was missing. Was there an <re> prefix in ‘reptile’? Of course not. This teacher was not missing anything, but her students sure were. They were missing the framework by which to understand the words they were being asked to read and write. They were missing being taught the structure (morphology), history (etymology), and using both of those to understand the pronunciation (phonology) of words. They were missing feeling comfortable to ask questions about things that don’t make sense (whether or not the teacher has a ready answer). The fact that students no longer ask questions about spelling by grade 4 should be a big red flag to teachers everywhere. Sadly it isn’t. The students have learned that the teacher won’t be able to answer or guide them to resources that would help anyway. They have no expectation that English spelling will make sense. That is sad. It doesn’t need to be that way.

My students don’t deserve to be limited by the boundaries of my own understanding.

Wood Farm Fence Clip Art And 4Vector

As teachers, we often feel more effective if we can anticipate the questions our students might ask and be ready with an answer. When we can successfully do that, we feel knowledgeable and think we are presenting ourselves as knowledgeable to our students. But there’s a catch to all that. In many instances teachers create a façade of having background in content knowledge. They have learned to rely on a teacher manual more than they rely on their own professional expertise. I don’t really want my students believing that I know everything or that I have all the answers. There are only a few students who would be brave enough to ask a question in that situation. Most fear looking “stupid” by asking a “stupid” question in the presence of someone who appears to be an expert, whether or not that is actually the case. If you’ve ever found yourself wondering why your students don’t ask more questions, perhaps you have set up this atmosphere without realizing it.

Here’s an example of a well meaning teacher who tried to limit her students to her own level of understanding. Each year I coordinate a Science Fair at our school. I’ve been doing it for years. (The simple reply to why I do it is that there are always those students who shine at the Science Fair in a way that is unexpected by adults/peers in their lives. Those adults could be adults at school who only see certain aspects of the student (math, reading, behavior issues, etc.), or they could be extended family or neighbors.) Anyway, one year there was a colleague who was guiding her own students through the process of getting ready for the Science Fair. She approached me and asked if we might change the scope of the Fair just a bit. Because she didn’t feel particularly knowledgeable about many areas in science, she was suggesting that we choose ten topics. The students could then pick one of those topics for their Science Fair project. In this way, she could anticipate questions and most likely be able to answer them as the students progressed through the weeks of experimenting. It would make participating in the Science Fair more comfortable for her.

As much as I understood why she was asking this, I couldn’t agree to it. It might eliminate the possibility of a student following a passion or interest. We all know what happens when a student is forced to pick a topic they are not interested in. That is not a way to encourage curiosity and creativity. When one of my students picks a topic I have no background in, I tell them how excited I am that we will both be learning about the topic. In fact, I find myself asking lots of questions when the student and I journal. (Since I am now the lone science teacher at our grade level, journaling is how I communicate individually with the 75 students I currently prepare for the Science Fair.) My own curiosity is aroused when a student picks a project or wonders about something no one else has picked or wondered about in the last 25 years of Science Fairs! Instead of limiting the students to my own background knowledge, I embrace stretching my background knowledge to include something new, and I model the enthusiasm that goes along with learning! It is very similar to how my students and I study the English spelling system.

My students and I find a sense of relief in the freedom that comes with not having to have the one right answer to every question. And yes, I included myself there. I never realized the “must know the right answer” burden I was carrying until I began investigating words. Since that day, I have moved forward as wide-eyed and curious as my students. I have experienced the joy of scholarship, and that has fueled a passion for desiring to know more. My students see me as someone who has a deeper understanding than they do, but also as someone who is eager to learn more. I make a big deal when a student asks a question I never thought to ask about a word or about a spelling. I make an even bigger deal when it is a great question that I don’t know the answer to. Just as in my Science Fair example, I am excited to know that the student and I will both learn something useful! My students are fully aware that I don’t know everything about English spelling. I am not setting up any false illusions about that. Yet we all understand that I am in the best position to guide the inquiries until they learn the process for themselves. And that is my goal – to teach my students how to use SWI on their own to deepen their understanding of the words they wonder about.

Here’s another example of a teacher whose students are limited in their learning by the teacher’s background knowledge. This is something I read on a blog the other day. The teacher is a kindergarten teacher who is teaching her students to read. She is enthusiastic and sincere in wanting her students to succeed. The task she describes is that of teaching sight words. First she says the word in question. Then she has them isolate the sounds they hear. Then she shows them the letters that represent those sounds by writing them on the board (orthographic mapping). She begins with the letters that represent a pronunciation that is predictable. Then she unveils the letters that represent a pronunciation in a way that isn’t expected.

“Sometimes I like to get a little dramatic as I unveil the word. -Especially for really irregular ones…my students died laughing when I revealed the spelling for “of” and showed the shock and craziness of the word with my expressions.”

If she herself had an explanation for the spelling of <of>, surely she would offer it. Since she doesn’t, she teaches her students that English spelling is often worthy of shocked looks and crazy expressions. When I asked why she embeds this rather unhelpful implication in her teaching of reading and writing, she defended it by saying that it made the sight words memorable and that the learning was fun this way.

Now I completely understand the idea of making learning fun and memorable. That is something I reflect on often in my own teaching. But I have learned to draw the line when what becomes memorable is a false premise for future learning. I understand that her goal for the school year is to have her students read and write. What she is doing will probably help her succeed in that. The method she is using is called Evidence Based Literacy Instruction (EBLI). I have no doubt that students being taught by this method leave kindergarten being able to do some reading and writing.

So if a goal as important as reading and writing is met, what’s the harm in her method? Well, let’s think about this. If she is teaching all “irregular” words in this way, she is sending the specific message to her students that many spellings are crazy and cannot be understood. And she is implying this over and over and over. By the end of the year, their overall impression of our spelling system is set. If the first grade teacher is also unequipped to explain words deemed “irregular”, then the students will receive a second year of subliminal messaging that “English spelling is unreliable and can’t be counted on to make sense.” What happens in second grade? More of the same? At what point are the students given the “straight skinny” about their spelling system? At what point do they meet a teacher who is willing to encourage their questions about why words are spelled the way they are and show them how to seek a deep understanding, knowing that what we understand is easier to remember? And if those students are lucky enough to encounter a teacher who can actually explain “irregular” spellings, along with supplying logical and predictable features of our spelling system, how on earth does that teacher have the time in one year to reset the attitude their previous teachers have nurtured? This is not a hypothetical situation. It is what I face every fall with each new fifth grade group.

Like I said before, I believe this kindergarten teacher’s desire to nurture successful readers is sincere. But in a really huge way, isn’t she limiting their understanding to her own? It is obvious that EBLI doesn’t offer any explanations for the spellings of sight words. If it did, this teacher would use them. Her heart is in the right place when it comes to doing right by her students. But how possible is it to be truthful right from the start with beginning readers when the teacher is missing so much herself? I often ponder this very idea because for years I didn’t question the idea of irregular words either. I just accepted that irregular words are words that can’t be explained and need to be memorized. This teacher is making that memorization fun, but in the end it is still just memorization. There is no understanding being offered. And I see a huge difference between “memorize this” and “understand this.”

Now let’s think for a moment about how a word ends up in the disgraceful “irregular” pile. It has to do with the alphabetic principle. We teach students that certain pronunciations will be spelled in certain ways using certain letters. When a word’s spelling deviates from that, it is labeled “irregular.” Some teachers (trying to make learning memorable) even shame the word by calling it “misbehaving.” There are even those who go so far as to put the word in “jail”. I love the fact that teachers are some of the most creative people I have ever met, but I also cringe when they use that creativity to disguise what it is that they themselves do not understand.

Unfortunately, too many teachers do not think young children are capable of understanding much about spelling. Their excuse is that we need to limit their cognitive load. Giving them a reason for a spelling, or planting any seeds about how fascinating and logical our spelling system actually is is out of the question in their minds. In my opinion, when adults decide what a child’s capacity for learning is (without having met the child), that child is instantly disadvantaged. If the only way to teach a child to read and write is to also teach the child that our spelling system is absurd and/or crazy, then I say find another way to teach reading and writing.

The number of classrooms in which children are being taught to read using SWI principles is growing every week. Age appropriate explanations are provided to children in regards to any word’s spelling. Right from the beginning, the children are taught to look for consistent spelling patterns, morphemes, and to recognize word families. They get lots of practice at recognizing grapheme/phoneme correspondences. They are encouraged to notice things and to ask questions. They enjoy making “word family” games for their classmates. And at the end of the school year, they are reading and they are writing. But most importantly, they are moving on to 1st grade expecting to read more, write more, and understand more about our language. No one has to back up the bus and convince them that spelling is in fact logical and fascinating. There is only a moving forward motion in their understanding! Each year they revisit important principles and ask the questions that deepen everyone’s understanding. They pull words out of context, investigate them at whatever level is appropriate, and notice other words that are related morphologically before putting the words back into context and discussing how understanding the word deepens its meaning within that context. Some of the very same things taught or practiced in an SWI classroom are also what is being taught with a method like EBLI. The major difference is the underlying belief that connects each year’s learning.

Imagine I had the choice of sending my young child to one of two classrooms. In both classrooms, there is a strong chance that my child would learn to read and write. The difference in the classrooms is this: In classroom #1, the students will learn that spelling, the system they will use the rest of their lives, is illogical and a lot of the times so crazy you’ll want to roll your eyes at it. They will memorize spellings without much understanding of why the word is spelled that way. They will be taught that some words have explainable spelling patterns and that many do not. They will practice sounding out words, and when a word can’t be sounded out, everyone will laugh at the word. In classroom #2, the students will learn that spelling, the system they will use the rest of their lives, is reliable and logical. They will immediately begin learning that words have structure and how understanding that fact will help them with building related words and spelling those related words. They will learn a “spell it out” strategy in which they identify bases and graphemes within those bases at the same time they are learning the word’s pronunciation and its spelling. They will learn that words have histories and that some words are very old. They will be encouraged to ask questions about what they notice about a word’s spelling. The teacher will help the students think through those questions.

I find it hard to believe people when they imply that it’s not possible to have the students leave kindergarten with the impression that there’s a reason for every spelling.
More and more teachers are proving the opposite of that every day. If you are interested in finding out more about what happens in those SWI kindergarten classrooms, I encourage you to participate in study groups with Rebecca Loveless and Pete Bowers. They have specifically worked with kindergarten teachers and their students.

It would be unrealistic to think we can teach without imposing (to some extent) the knowledge limits we each have. But isn’t it our responsibility to constantly reflect on how our own limits affect our students? I don’t like to think that I’ve invited my students into my yard (if we can think of my background knowledge as a yard with fences) and that they become prisoners there. Or that if they ask questions about what is beyond that fence, I would need to make up cutesy explanations to keep them from exploring what I myself am not comfortable exploring. I would rather think of this as me inviting them into my yard, and then when they ask questions about what’s on the other side of the fence, me going with them and modeling how to search for understanding. In the process I would be showing them how to keep expanding their own yard by continually moving those fences. When I am willing to either step outside my “fence” or to keep extending it, we all benefit as learners.

And here’s another thing that doesn’t often get considered. Never forget that students are as deep-down satisfied to prove truths about our English language to themselves as we are! When you spend year after year in classrooms in which the teacher is the expert, and you and your classmates are the buckets to be filled, this kind of investigating can be exhilarating! Students find it refreshing, really, to be given the tools and the opportunity to raise a question and then to prove or disprove it to themselves. My role becomes that of a guide, steering the questions the students have during an investigation back on them as often as possible, but also realizing when they have reached a point where they are truly stuck.

I might also add that I know of several adults with dyslexia who have shared with me their experiences of learning to read in school. They were frustrated much of the time because they were asked to remember bits and pieces without a context. Being told that our language was absurd or crazy made learning to read and write even harder because in effect they were being told it didn’t make sense. Being given a solid understanding of the interrelationship of morphology, etymology, and phonology, however, has turned a truly laborious task into a fascinating one. I’m not saying that their dyslexia has disappeared, but I am saying that they no longer feel as if they are staggering in the dark. Those adults ask lots of questions and think through lots of their own hypotheses thanks to finding Structured Word Inquiry. And every one of them is sharing their understanding with children. They, more than almost anyone else, really get what a difference understanding the spelling system can make.

Doing what is right for children isn’t easy when you are swimming against the educational current. When you have the guidelines of Structured Word Inquiry, when you can see for yourself what is true, and when you can provide evidence to any doubtful package-loving administrators, you do so, and then you just keep swimming. It’s what you do.

Image result for swimming against the current

April 18, 2019 by mrssteven

Instead of Being Submerged in a Sea of “Sound It Out”, We Suggest Spelling Success with Structured Word Inquiry!

My students have been working on several things lately. Some have been looking at specific graphemes/digraphs and the phonemes that they can represent. Others have been looking at prefixes and the assimilated forms they often have. Still others have begun to explore Latin verbs and the unitary/twin bases that come from them. So with all of these different investigations going on at once, how do I make sure that all the students are learning all these things? It happens on a day like today. It happens when I plan a simple review that turns into a simply rich inquiry. I can’t imagine that any other review set up in the same way would yield anything less. You see this wasn’t a fluke. It didn’t just happen once today. It happened three times … in each of my three classes. Fortunately I set up my camera during one of the classes and am able to invite you in. If I tried to tell you all about it without letting you see for yourself, you might think I was exaggerating.

Setting the scene …

Here are a few of the posters my students have presented lately. When I say they presented the poster, I mean they told the class what their investigation was all about. They read any words they found that were related to the investigation, and then they shared the definitions of some of the words that were new to them as they investigated. After that, the students listening asked questions and discussions ensued.

With other investigations still in process, I thought it was a good time to pause and reflect on what we have been learning. Every once in a while I see the students sliding back into the comfortable yet unproductive habit of robotic research. I define that as collecting what has been asked for without thinking about what the words mean or whether or not they fit the focus of the investigation. Their whole spelling lives they have been asked to mindlessly focus on letters and letter strings. They have not been asked to see those letter strings as anything in particular. I am asking them to think critically about whether those letter strings constitute a morpheme in a word. This is a new skill for most.

Before the students walked in, I wrote the prefix <sub-> on the board along with the most common sense it brings to a base, “up, under.” Then once the students were seated, I asked them to think of words with a <sub-> prefix. It could actually be , but it could also be one of this prefix’s assimilated forms (<suf>, <sug>, , <suc>, <sur>). Here is what the board looked like:

At this point I asked the students to look at the board and let me know what they thought. Did all of these words indeed have an <sub-> prefix or one of its assimilated forms? Is there anything you question or wonder about?

I turned on my camera and the students were engaged in discussion for 50 minutes. Fifty minutes! Take a listen and see where their questions and observations took the discussion. (Don’t worry. I edited so that the first video is 12 minutes and the second is 7 minutes. I must say it was hard to find parts of the discussion to cut. It was all as great and interesting as what you are about to see!)

As you can see, the questions just kept coming and the students exhibited a comfort level in using the resources (on this day it was Etymonline and the Collins Gage Canadian Paperback dictionary). They were connecting dots all over the place! They were understanding familiar words in a new way and understanding unfamiliar words enough to connect them to other words by their structure. Structured Word Inquiry is never about memorizing a word’s spelling. It is about understanding it. But becoming a better speller is a pretty reliable side effect of the work my students do each day. We talk about words every day whether we are focused on SWI or not.

When my third group of fifth grade students brainstormed their own list of words with the <sub-> prefix or one of its assimilated forms, this is what the board looked like. I did not take video, but you can imagine by what you see that it was every bit as rich a discussion as with my middle class. You’ll notice that some of the same words were thought of by students in each class, but then there were words that didn’t appear in the last group’s discussion. Is that important? I don’t think so. We focused on the meaning and structure of the words. And when we needed it, we went to a resource to find out which language the word originated in and perhaps what other languages had an effect on its spelling.

You will notice that we crossed off the words <sucking> and <super>. It was in a quick discussion that a student explained why the <suc> in <sucking> couldn’t be a prefix like we see in <success>. In the word <sucking>, the students recognized that the base was <suck> and that the <ck> was representing one phoneme, /k/. The students decided that if <super> had an prefix, that would leave <er> which is a pretty common suffix. But then there wouldn’t be a base! As I did with the other class, I had someone look up the word <super> to verify that the was indeed part of the base and NOT a prefix. As it turns out, this word is from Latin super “above, over, beyond.” This word is a free base and it’s spelling hasn’t changed at all! We talked about superheros and supervisors and how that denotation of “above, over, beyond” made sense.

That brought us to the word <supper>. Everyone was familiar with supper being a meal eaten in the evening. One hypothesis was that the prefix was and the base was <per>. Another was that the prefix was , the base was , and that the suffix was <er>. I had someone go get a dictionary. That person reported that the base was with a denotation of “dine.” That meant that the <er> was a suffix and the second was the doubled from when the vowel suffix was added. They were not familiar with the base , so I reminded them of the base <hap> that we see in <happy>. A very similar thing happens in that word. So even though the in <supper> is followed by a , that doesn’t mean it is a prefix. In this word, the is the base! It’s a third word we could have crossed off.

Since we had just found a word in which the was a base and the that followed it was the doubled , someone wondered if the same thing was happening with <supply>. They asked if was the base and there was an <ly> suffix. But then someone else pointed out that <ly> is a consonant suffix and wouldn’t cause doubling. (It is so amazing and wonderful to watch one student’s understanding broaden another student’s understanding!) So then the student who had raised the question went to get a dictionary to find out whether or not the base was <ply>. The student found out that in this word, the prefix has a sense of “up” and that <ply> is from Latin plere “to fill.” Someone immediately thought of buying school supplies. Someone else thought of the way the school supplies desks and chairs for the students. Both are example of items that fill a need.

From <supply> we went directly to <supplement>. I wondered aloud what a supplement was? Someone was familiar with a supplement being extra sheets of ads that comes with their newspaper. I mentioned that I sometimes take a supplement. I sometimes take a vitamin C tablet. Several students nodded and shared that they sometimes do too, like when they have a cold. So we came to the understanding that a supplement is something added to something else. When a student looked in the dictionary, the student found out that <supplement> is from Latin supplere “to fill up.” Then the entry said, “See supply.” Aha! This is the same Latin base we saw in <supply>!

Another interesting word was <submarine>. The students were pretty confident that was the prefix here because they knew that a submarine was a vessel that went under the water. So I asked if they thought <marine> would be the base or whether it could be further analyzed. It was quiet for a bit while everyone gave it some thought. Then someone said, “Could the <ine> be a suffix like in <saltine>?” I added, “And <routine>.” Hmmm. A student once again offered to look up <marine> to see what evidence there was to help us with identifying the base. The student found out that it was from Latin mare “the sea”, which really made sense to everyone seeing as a submarine goes under the sea! Could we think of any other words with <mare> as its base? I thought of <maritime> which I explained as having to do with the sea. I could say that a dolphin is a maritime mammal, meaning it lives in the sea. Then, when I was just about to move on, someone suggested a student’s name. Marissa. I had no idea if that would share the base or not. It shares spelling, but that doesn’t necessarily mean they share meaning. So I told Marissa to get a Chromebook and find out what her name meant. Sure enough! It comes from the Latin maris “of the sea!” How about that?

Reflections …

In each of my three classes we started the same way, but then followed the path led by their questions. Over and over we talked about the prefix and the sense it brought to each of the words it was part of. We made great discoveries about some unfamiliar bases, both bound and free. We even talked about twin bases when the opportunity arose. They eagerly jumped up to get a dictionary when we were ready to understand a word’s structure better. We connected the literal meanings of the base and prefix to what we understood the words to mean in our daily lives. We stretched that understanding to other words with the same base when we could. Most importantly, the students looked critically at the words and determined for themselves whether or not there was an <sub-> or other assimilated form of an <sub-> prefix. When the letters at the beginning of the word were found not to be a prefix, the students could explain why that was.

This kind of critical thinking, this kind of scientific inquiry comes without judgement. Students offer suggestions without the fear of being wrong and the embarrassment that goes along with that. Everyone has the same pursuit, which is to make sense of a word’s spelling. And everyone participates in that common pursuit. Some think to themselves. Some think out loud. Some ask questions. Some jump at the chance to look something up in one of our dictionaries or at Etymonline. The engagement is high and the delight in discovering something about a word or a connection being made is often audible. (And usually accompanied by a sweet smile!) This is what I have always imagined learning to be like! As Malina said at the end of the second video, “Every single time that someone comes up with an idea, we should put a little light bulb above their head.” Man would there ever be a glow coming from our room!

March 26, 2019 by mrssteven

Having a Blast! Creating a Podcast!

When a colleague forwarded a notice back in January about a podcast contest that NPR was hosting, I was immediately interested. It sounded like something my students and I would enjoy doing. The fact that I had never created a podcast before didn’t deter me. Back when I was doing my own student teaching, I had my students create radio shows. Wouldn’t this be similar?

The idea of having the students prepare a script that didn’t rely on visuals was appealing. They would have to make sure they spoke in ways that complemented what they were saying. They would have to think about the words they were using and not just assume that the orthography terms they use every day would be familiar to their listener. They would have to rehearse, rehearse, rehearse so that they sounded more like they were speaking than reading. And in my mind, I knew they would need to write a script that was longer than anything they’ve written to date! What a lovely marriage of research, writing, revision, reading, speaking, and collaboration this could be!

Podcast Microphone

NPR supplied a well-thought-out plan for guiding educators and students through this process, so I decided to present this idea to my students. Since I teach three groups of 22 students each, I wondered how many of the students would be interested. I needn’t have wondered. It turns out they were ALL interested! Okay! We were in!

We began by listening to some of the podcasts recommended by NPR. We listened to one a day for several days, pausing to discuss the kinds of information we felt was important to have been included, the overall feel of the podcast, the seriousness of the overall information sharing, even when humor was involved, and the sound effects. Each day, the excitement grew in regards to writing their own. Many were regular podcast listeners and were especially enthusiastic. The majority of students, though, had never listened to a podcast before this. But they too became enthused as they listened to the well-put-together podcasts each day.

The first thing we had to do was think of our topic. For me, that was obvious. The students would be randomly placed in groups and would each investigate a word of the group’s choosing. They loved that idea! The students had investigated words on their own several times and were familiar with the resources to use. This idea gave them a level of comfort as they began. Putting them in groups of 4-5, meant there were five groups in each class. That meant we would be creating a series that included 15 podcasts. The students wouldn’t just be looking at the word’s etymology or root, they would also be looking at how the word’s use or spelling might have changed over time. It would also be important to include current information about this word’s meaning and its use. In other words, they would be providing a broad look at a single word. This was going to require a lot of research before script writing could even begin!

The students took a few days to think about what word they would choose. Some were inspired by what they had been learning about during their study of the Civil Rights Movement (segregation, peace). Others brainstormed a list and then looked up information on each to see which sounded more interesting to them. One group paged through a copy of John Ayto’s book, A Dictionary of Word Origins, and found their word (eureka). As soon as each group had decided, they let me know and then started learning as much as they could. As they found out things, they shared the information with the group.

Several days in, each group started writing a script. According to the NPR guidelines, the podcasts were to be a minimum of 2 minutes long with a maximum length of 12 minutes. These scripts were no doubt the longest scripts any of these students have been a part of writing! When they would tell me they were finished, I would ask them if they timed themselves practicing their podcast. When they did, they would realize their podcast was too short. So then the real digging began. The search for related words. The search for changes in spelling over time or changes in meaning over time. The search for the word to be used in different ways depending on a context. The search for how the word is used today and perhaps which people have become associated with the word.

And with this renewed digging, this need to find more, came some surprising facts which were surprisingly satisfying! I could feel the level of engagement increase among the students. They would enter my room each day with the same question ready for me, “Are we going to work on our podcasts?” After a quick progress check (making sure each person knew their role and each group was focused), they grabbed their Chromebooks, found a table or grouped desks together and got to work.

Every once in a while I would hear an extended patch of laughter coming from one or another group. When I went over to check it out, it was always related to their script or the misreading of it or some information they found that seemed funny. They were still engaged, just enjoying the team work atmosphere and the shared experience of creating something worth creating!

A few groups included interviews. The group that was looking at “segregation” interviewed their social studies teacher. The group that was looking at “frog” interviewed me. (My fondness for all things “frog” is obvious to those who enter my room!) And the group that was looking at “lexical” interviewed the creator of The Online Etymology Dictionary, Doug Harper. That interview was something we all benefited from. It was a Zoom (online) interview and the whole class was able to meet and listen to Mr. Harper!

After three weeks or so (I kept reassuring them that the research and writing should be the most time consuming of any part of this project) the first of the groups finished, and said they were ready to record. It was time to start the next phase of this project.

According to the guide at NPR, I could have recorded these audio files on my iphone, but with 15 groups, I could imagine running into problems with space on my phone. So I purchased a recorder. I’m so glad I did! I would get it set up for the students and they took it from there. Most all of the groups recorded more than once. That was fine. We were all getting used to the equipment, being loud enough, being slow enough, and having enough expression in our voices. We turned a small storage room into our “recording studio.” You can see my recorder on the inverted tin can in the center. The students read their scripts from their Chromebooks so they wouldn’t have to worry about the added sound of papers shuffling.

Next we went down to the computer lab and uploaded the audio file into Audacity which is a free software for editing audio files. The students had never used Audacity before, and neither had I. So the students learned to use the HELP tab. When they couldn’t find their answer there, they tried looking for a video at Youtube that would walk them through editing at Audacity. Sure enough! They not only found answers, but could watch someone do what they needed to do. They became pretty confident at editing and offered help to other groups who became stuck. So not only was I seeing cooperation within the groups, I was seeing cooperation between the groups! This experience just kept getting better and better!

The trickiest part of this editing was that at some point we had five groups in the lab all trying to listen and edit their podcast. If headphones were used, that meant that only one person would be making decisions, so the groups usually used headphones only for listening to the instructional videos at Youtube.

But one by one, the groups finished the editing and I saved the file to a flash drive. Then it was back to the classroom for the group. Once they finished their podcast, I asked them to present their same script as a video. They now had the opportunity to add pictures, images, and matrices to enhance their information. This seemed like another way to share their word investigations in a slightly different platform!

As the groups finished, I uploaded each podcast to SoundCloud. From there, NPR will be able to access them as part of their judging. Then I filled out the entry form for each group. They will be judged in the 5th-8th grade category. Will one of these podcasts win? Who knows. All I know is that in the hearts and minds of my students, they have already won. When I hear students say, “I am really proud of our group! I’m proud of me!” then I know that this learning experience has been rich and worthwhile. We all know that learning isn’t just about learning the content. And this experience was no different. These students had to persevere when the editing got confusing or they just couldn’t figure something out. They had to ask for help when needed because this project had a deadline and there wasn’t time to waste. They had to use patience when one member stumbled over speaking parts or pronunciation of words. (They were so helpful and kind to one another and never minded practicing just one more time before recording.) They had to be willing to go back and re-record if the group felt that was the best option. You see, with every group I saw a serious goal of turning in the best version of their podcast that they could. I was constantly proud of their attitude, work ethic, and respect for members in their groups. Were there moments of chaos and discord? Absolutely! But all in all, the students learned to redirect their attention, be accountable for their contribution to the group, compromise with members in their group, and compliment each other for little things done well!

In other videos my students have created, I have been the script writer. This time the students can proudly say they did every facet of this project themselves. Mind you, if I noticed that something was incorrect or mispronounced, I spoke up and the students willingly amended their podcast. But I’m sure I missed a few things as well. Just today I was listening to the episode about “Eureka!” About three fourths of the way through, I realized that the name of the city they were mispronouncing was Syracuse! Made me chuckle. Their mispronunciation made me think at first that it was a city I didn’t know! It is still one of my favorite podcasts in this series. Okay, so in truth I have around 15 favorites in this series!

Here is a link to my SoundCloud channel. I hope you will listen to a few of these podcasts. If you are wondering where to start, you might enjoy “Lexical” which has the interview with Doug Harper. Some other great ones are “Hippopotamus,” “Not so Nice,” “Kerfuffle,” “Eureka,” and, well, all of them! You can either listen here by clicking on the arrow in the top left corner, (in which case the podcasts will play in the order they are listed) or you can click on my name and it will take you to my page on SoundCloud where you can see the full name of each episode and choose the one you’d like to listen to. You can also scroll through the list below my image and choose one (although the full name of each episode isn’t always showing.)

If you prefer the video versions, there are about four finished so far. I am busy editing more and will be adding them to my Youtube channel in the next two weeks. Here is a link to my Youtube channel:

https://www.youtube.com/user/MaryBethSteven/featured

February 8, 2019 by mrssteven

“Button up your overcoat when the wind is free….” Ruth Etting

It’s all well and good that we can put on an extra layer when the wind gets chilly and the temperatures drop, but what do the wild animals do? How do they cope with the heavy snow and freezing temperatures? That is the focus of the article I read recently. It’s called “Do Wild Animals Hate Being Cold in Winter?” It was published in Popular Science, written by Bridgette B. Baker. You can read it at THIS LINK.

As I read it, I couldn’t help but notice a number of words that share the base <therm>.

“In fact, wildlife can succumb to frostbite and hypothermia, just like people and pets.”

“One winter challenge for warm-blooded animals, or endotherms, as they’re scientifically known, is to maintain their internal body temperature in cold conditions. Interestingly though, temperature-sensing thresholds can vary depending on physiology. For instance, a cold-blooded—that is, ectothermic—frog will sense cold starting at a lower temperature compared to a mouse. Recent research shows that hibernating mammals, like the thirteen-lined ground squirrel, don’t sense the cold until lower temperatures than endotherms that don’t hibernate.”

“Many cold-climate endotherms exhibit torpor: a state of decreased activity. They look like they are sleeping. Because animals capable of torpor alternate between internally regulating their body temperature and allowing the environment to influence it, scientists consider them heterotherms.”

Most people will acknowledge these are interesting words. But when summarizing the information, they will skip using them and go back to using simpler, more familiar language. Often the thought is that these words are too tough for children to remember (especially if the adult doesn’t really understand what they mean). What if instead of skipping using them, we investigated them further? What if we looked closer at the sense, the meaning and the function of the morphemes in each of these words? We have here an opportunity to understand scientific terminology AND word families better!

hypothermia

Let’s begin by looking at <hypothermia>. It was first attested in 1877 and is from Modern Latin. When something is noted as being Modern Latin, that means that the word was created by scientists who needed a name for something. They didn’t just make up a name, but rather they looked back to Latin and Greek for what to call it. The word <hypothermia> did not exist in Greek, but the stems <hypo> “under” and <therm> “heat” did. The <-ia> suffix indicates that this word is an abstract noun. If you look at the denotation of the base <therm> “heat” and the denotation that the base <hypo> “under” has, you can see that the word itself tells you that hypothermia is when something is under it’s normal level of heat. If a person has hypothermia, their body temperature is lower than it should be. The base <therm> is from Greek θερμός (transcribed as thermos).

What about this base <hypo>? It is from Greek ύπό (transcribed as hypo) and has a denotation of “under.” Have we seen this in other familiar words? What about a hypothesis, which is the groundwork for an investigation. Do you recognize the denotation of “under” in hypothesis, as in an underlying position? It is also in hypodermic, which is the area just under the skin. That gives you a better sense of where a hypodermic needle is used, doesn’t it? And what about hypotenuse, which is the side of a triangle that is opposite the right angle. It has a sense of being stretched under the right angle.

endotherms

When I looked for <endotherms>, I was lead to <endothermic>. Etymonline notes that this word was first attested in 1866 and was formed by adding <endo-> and <thermal>. The suffix <-ic> indicates that the word is an adjective. The suffix <-al> can indicate the same thing. When I look at the entry for <thermal>, I learned that the first time it was used to mean “a sense of heat” was in 1837. So using <-al> is older than the use of <-ic> with this base.

So what about the base <endo->? It is from Greek ένδον (transcribed as endon) and has a sense of “inside, internal”. When you pair up <endo> “internal” and <therm> “heat”, you can see that the word itself tells you that endotherms are organisms that regulate their heat from inside themselves.

We see this base in endoscopy which is when a doctor uses a camera and light attached to a flexible tube to examine your esophagus, stomach, and/or intestines. In other words, the doctor is looking at your internal organs.

This base is also in endoskeleton which is the internal skeleton structure that all vertebrates have.

My dogs are endotherms. So am I.

ectotherms

There was not a specific entry for <ectotherms> at Etymonline, but there was an entry for <ecto->. It is from Greek έκτός (transcribed as ecktos) and has a denotation of “outside, external.” It is related to the prefix <ex-> “out”, but they are not the same. When you pair up <ect> “outside” with <therm> “heat”, you can see that the word itself tells you that ectotherms are organisms whose body heat is regulated by their environment (outside themselves).

I went to the Oxford English Dictionary (OED) to find related words. This base is found in science words like ectotrophic. An example of that is when tissues form on the outside of a root and are being nourished by that root. Interestingly enough, the opposite of ectotropic is endotrophic! That is when one organism is getting nourishment from within another organism.

We also see this base in ectocrine which is described as an organic substance that is released from the outer layer of an organism that will effect other organisms in the environment in either a good or bad way. It will come as no surprise to you that this word is the opposite of endocrine, which is a gland having an internal secretion. So in one case the secretion is external, and in the other it is internal.

Turtles and snakes are ectotherms. They bask in the sun to get heat.

heterotherms

There wasn’t a specific entry for <heterotherms> at Etymonline, but there was an entry for <hetero->. It comes from Greek ’έτερος (transcribed as heteros) with a denotation of “one of two”. When you pair up <heter> “one of two” with <therm> “heat”, you can see that the word itself tells you that heterotherms are animals that can regulate their own heat AND also have their heat regulated by their environment. Here’s something interesting that I found at Wikipedia:

“Regional heterothermy describes organisms that are able to maintain different temperature “zones” in different regions of the body. This usually occurs in the limbs, and is made possible through the use of counter-current heat exchangers, such as the rete mirabile found in tuna and certain birds. These exchangers equalize the temperature between hot arterial blood going out to the extremities and cold venous blood coming back, thus reducing heat loss. Penguins and many arctic birds use these exchangers to keep their feet at roughly the same temperature as the surrounding ice. This keeps the birds from getting stuck on an ice sheet.”

“Chinstrap Penguin with snow in its mouth” by Liam Quinn is licensed under CC by-sa 2.0

Here is a matrix of the words we have looked at:

You will notice that all the base elements are bolded. The connecting vowel <o> and the suffixes are not. That means that there are four compound words represented on this matrix:

<hypothermia –> hypo + therm + ia>
(or variations such as hypothermic or hypothermal)
<ectothermal –> ect + o + therm + ic>
(or variations such as ectotherm or ectotherms)
<endotherms –> end + o + therm + s>
(or variations such as endotherm or endothermic)
<heterotherm –> heter + o + therm>
(or variations such as heterotherms or heterothermal)

You may not be familiar with a connecting vowel, so let me explain a bit about them. They are used to connect two bases (as they are doing in three of the four words above), but they can also connect a base to a suffix or a suffix to another suffix.

My favorite example of a compound word with an obvious connecting vowel is <speedometer>. We instantly recognize the two bases here because they are both free bases. We also recognize that the <o> doesn’t belong to either one! It is simply connecting them. The <o> can be used because the second base <meter> is from Greek μέτρον (transcribed as metron) “measure”. The first base is not from Greek. It is from Old English sped. The sense and meaning “rate of motion or progress” is from c.1200. The fact that one of the bases is from Greek and one is from Old English makes this word a Germanic hybrid!

Have you noticed that in the above matrix not all of the words have an <o> connecting vowel? How do I know that the <o> at the end of <hypo> is not a connecting vowel? I start by doing some research. If you skim back through the paragraphs in this post, you will find that the origins of the bases are as follows:

<therm> – Greek θερμός (transcribed as thermos)
<hypo> – Greek ύπό (transcribed as hypo)
<end> – Greek ένδον (transcribed as endon)
<ect> – Greek έκτός (transcribed as ecktos)
<heter> – Greek ’έτερος (transcribed as heteros)

Notice that three of the four have the same Greek suffix. That <os> suffix is called the nominative suffix. If I remove it, I see the stem that then came into English as a base. There is one word that has a Greek <on> genitive suffix. If I remove it, I see the stem that then came into English as a base. Those four bases entered English without the <o>. We can also notice that the words we’re looking at today were coined by scientists who needed a word to describe something they were working on. Oftentimes they joined the Greek (or Latin) bases (that fit best in the context of what they were doing) with a connecting vowel.

I know that <hypo> does not have a connecting vowel because it does not have a Greek suffix that could be removed. This present day base was a preposition in Greek. If you look in the OED, you can find several entries for <hypo> as a free base noun.

The bottom line

As you read through this post, I hope your sense of these bases deepened. When I do this with children, it’s not that I want them to remember every word we talk about. It’s more that I want them to take an invisible thread and connect each base or morpheme that we focus on to the words in which it is used. I want them to see that every word is not completely new and unique. Words belong to families, and the key to understanding an unfamiliar word is by recognizing one or more of its morphemes and being able to recall some related words to help with remembering the sense and meaning that the words share.

The matrix I created above focuses on the words from the article that had the base <therm> in common. The joy of matrices is that they can be used for what you need them to be used for. They don’t need to contain every possible word that shares the base (probably impossible anyway). I love when one of my students presents a matrix they made to the rest of the class and another student asks, “Could such and such a word be added to that matrix?” The person who created the matrix doesn’t have to feel embarrassed because they missed something. There is no expectation that a great matrix has x number of words! A word matrix is a starting point. It is a thought provoker and a discussion starter. When another student suggests a word that could be added, it proves that the students in the audience are engaged and thinking about this particular family. That is a thing to celebrate!

That being said, a fuller matrix is really fun to look at once in a while. Once you start thinking about this base <therm>, you start wondering what other words you know that share the base. Have fun thinking about the words represented below. Do you recognize the bases we just studied? Do you recognize the others? Are you familiar with the suffixes? Are you noticing that a connecting vowel is used to connect bases where <therm> is the second base? Are you noticing that a connecting vowel is used to connect bases where <therm> is the first base? Are you aware that any word that contains two or more bases is a compound word? Do you know the denotations of the bases I haven’t talked about?

I encourage you to use Etymonline as a starting point. Find out what the bases mean independently, and then find out how we currently use the word by looking in a modern dictionary. Sometimes I like to search for an image as well to further deepen my understanding. Notice how the connecting vowel is pronounced in thermographic, thermoluminescence, thermostat, and thermosphere. Then notice how there is a shift in stress, which changes the way we pronounce that connecting vowel in thermography and thermometer. Interesting, right? The pronunciation changes, but the spelling and the meaning does not. An orthographic truth you can count on!

A warm send off

Well, this here endotherm is going to put on thermal underwear so she doesn’t have to turn up the thermostat. I wish we had geothermal energy, but we don’t. Staying warm might prevent the need for a thermometer should she take a chill. Once she’s dressed in layers, she can gaze out the window and imagine that she can see all the way to the thermosphere.

December 11, 2018 by mrssteven

Conferences: An Opportunity to Get the Word Out

This is what I shared with the parents of my students at our recent set of conferences. Since those conferences were scheduled three weeks before the end of the trimester (which meant that my grades were not yet finalized) I used the opportunity to explain what I teach under the heading of orthography.

I began by explaining that one of my goals is to teach students why words are spelled the way they are. A word’s spelling is primarily representing meaning, and not pronunciation. An example of what I mean by that is the word <goes>.

On the day after our final performances of The Photosynthesis Follies, I gave a photosynthesis test. As I was correcting the tests, I couldn’t help but notice that more students than I would’ve thought, misspelled <goes>. Five students spelled it as *<go’s>, two students spelled it as *<gos>, three students spelled it as *<gows>, three students spelled it as *<gose>, and one student spelled it as *<gous>. Sometimes when I mention to colleagues that students struggle with spelling, their first reaction is to say, “They need more phonics! Those lower grades must have stopped teaching phonics!” But I say no. It is pretty obvious that the students have learned to spell phonetically. Anyone reading their work can guess what word they intended to spell. They are spelling using the only strategy they’ve been taught: Sound it out. And if we started naming words that are similarly difficult to spell accurately using only “sound it out”, we could name quite a few. Don’t you agree? So what now? If the problem isn’t phonics, what is it?

Well, what if, when we were teaching our students that graphemes represent pronunciation, we also taught them that words have structure? What if the students were taught to look at this word and recognize that <go> is at the heart of its meaning? We could teach them that this word starts with its base element, <go>, and if we want to form other words using this same base element, we could add suffixes. If the child is learning the spelling of <goes>, he/she is probably familiar with the words <going> and <gone> as well. We could teach the student that <go + es is rewritten as goes>, that <go + ing is rewritten as going> , and that <go + ne is rewritten as gone>.

If we look at other word families in this same way, it won’t take long before the student has learned some of the more commonly used suffixes and prefixes. So even with early readers, recognizing some part of a word will help when encountering unfamiliar words. When decoding, the student can focus on the base element in the word because they recognize a suffix they can remove.

So now let me show you what I am doing with fifth grade words. We begin our science curriculum by studying the interactions of the biosphere, geosphere, atmosphere, and hydrosphere. As an orthographer, I immediately noticed that this group of words shares a structure. Focusing on that structure, I added lithosphere, troposphere, stratosphere, mesosphere, thermosphere, and cosmosphere to the list. I had the students investigate these words in small groups.

They are all compound words. You can see the familiar base <sphere>. Just in front of that base you’ll notice that each word has the connecting vowel <o>. That leaves a rather unfamiliar looking base at the beginning of each word. It looks unfamiliar because we have not been taught to recognize bound bases. A bound base is not found as a word on its own. It is always bound to another element in the word. When we think of compound words, we think of words like chalkboard or hallway. In those words we see two free bases joined together. In biosphere, we have a bound base <bi> joined to a free base <sphere> by the connecting vowel <o>. This <bi> is from Greek and has a denotation of “life”. The second base <sphere> is from Greek too. It has a denotation of “globe”. So the biosphere is everything that is alive on our globe or planet.

It is great to better understand a word by looking at its structure, history and the overall meaning we glean from paying attention to its elements. But if we stop there, we are only giving a student one more word to remember. Instead, looking at a word’s relatives is how a student makes connections to other words and how a word’s meaning becomes memorable. If we continue to look at <biosphere>, and focus on the first base <bi>, we can find words like <biographer> “someone who writes about other people’s lives”, <biohazard> “something that is dangerous to living things”, <biology> “the study of living things”, and <bioluminescent> “living organisms that emit light”. Do you see how all of these words are connected in meaning? If the students begin to recognize a base like <bi>, they will have a hint at what an unfamiliar word like <biometry> might mean. At the very least they will know it has something to do with “life, living”. If they also know the second base in this word (<meter>) has to do with measuring (geometry, diameter, speedometer, kilometer), they will put the two meanings together. They might still need clarification as to what it means to measure life, but a quick look at Etymonline will tell them that biometry is the calculation of a life expectancy. A biometrist tries to calculate how long something (under certain conditions) might live! Cool!

**At this point I encourage the parents to take a look at the posters in the hallway (once we have finished with the conference). The posters show the various investigations by the students. I feel it is important to also point out to the parents that when they look at the posters they should keep something in mind. It is not my intention for the students to remember all of the words they find. Rather, it is my intention for the students to realize how many words can be related to one base element and its shared denotation! Then, of course, the students also begin to realize that all words have structure (morphology), and a history (etymology).

Next I showed parents the list of these words that was still on the whiteboard in the classroom. The students had written the year each word was first attested next to its corresponding word. It is my intention to have the students make a timeline to better organize the words and their attestation dates. Then we’ll be able to talk about which word was around first and which was created most recently. As it turns out, the word <atmosphere> was first attested in 1630. It is interesting that the oldest of these is <atmosphere> “gaseous envelop surrounding the earth.” It just goes to show how long scientists have been looking up and wondering about our atmosphere.

As the years passed and the technology became more advanced, scientists were able to detect differences in different areas of the atmosphere. It became important to be more precise in what they called things. I find it interesting that the specific layers of the atmosphere were named so recently. It began with the stratosphere in 1908, the troposphere in 1914, the thermosphere in 1924, and the mesosphere in 1950. You can almost imagine the scientists making their observations and then realizing that the atmosphere was actually made up of layers, each with unique properties. And as there was a need to fittingly name each layer, they looked to the classical languages (Greek and Latin) for appropriate elements!

The next topic we discussed was the teaching of Chancery Script. My goal is for the students to have consistent and legible writing that also reflects their personal style. I have fountain pens that we use when practicing. We focus on writing posture and a comfortable pen hold (as opposed to a tense grip). Again, I direct the parents to stop on their way out and see the examples I have posted in the hall.

When I moved on to what the students were learning in science, we ended up weaving in orthography once more! As we’ve taken a closer look at the biosphere, we’ve learned about food chains and food webs. The Photosynthesis Play we recently performed for the school, gave us a good start in understanding that the sun provides the energy for photosynthesis. In fact, the word <photosynthesis> means “put together with light”. It is the Greek base <phote> that means light. We see this base in photography, photojournalism, photocopy, and phototropism (since we’ve studied the word <troposphere>, we know that phototropism has to do with a plant turning towards the light). We have also studied the word <synthetic> and we use it often when we write synthetic word sums. We know that a synthetic word sum is one in which we put the elements together to form a completed word.

Because of our previous understanding of the words <synthetic> and <phototropism>, we could more easily understand that <photosynthesis> would be a combination of those meanings “put together with light”. Quite by coincidence, a few days later we were watching a video that further explained food webs and trophic levels. The narrator in the video spoke about photosynthesis (the process in which a plant produces its own food), but then added that some bacteria are too far from the sunlight’s energy, and so produce their own food using chemosynthesis. Without skipping a beat, several students raised their hands and excitedly explained that chemosynthesis would mean “put together with chemicals!”

I love presenting words to the students that I know they will be unfamiliar with, but that share a base we have talked about. In this way, I am teaching the students to look for familiar elements in a word. Of course, I also teach them that while creating a hypothesis about a word’s structure is a great thing to do, checking a reliable source to confirm or falsify that hypothesis is a responsible habit to form! To this end, we use many etymological and regular dictionaries on a daily basis.

The study of food chains, food webs, and trophic levels exposes the students to many great words and word families. If the organism makes its own food, it is a producer. If it eats the producers, it is an herbivore. If it eats an herbivore, it is a carnivore. If it eats both producers and carnivores, it is an omnivore. If the organism has no natural predators, it is a top predator. If it is not a producer, it is a consumer. If it eats an organism’s waste, it is a detritivore. If it helps break down a dead organism it is a decomposer.

So how do I help my students understand those words when there are so many? We look for related words. We look at their structure. We look at their histories.

This first matrix shows how carnivore, detritivore, herbivore, and omnivore are compound words and share a structure. They also share the base <vore> “devour”. As you can see, the words voracious and voracity are also represented on this matrix. The students may not know these words, but it makes sense to introduce them as other members of this family. It deepens the connections being made. I might even ask them to name a time they had a voracious appetite!

In this matrix I’ve chosen to include three related words (with options for suffixing). I am illustrating this base in other words besides the one we are focusing on in our study (producer), but I choose not to overwhelm the students with too many unfamiliar words this time.

In this matrix, I am sticking to one word and its suffixing options. I use a matrix like this to practice the suffixing convention of replacing the single final non-syllabic <e>. I also use it to point out that suffixes can have grammatical functions.

As we are finishing up our time together, I once again point the parents to the display that is up in the hallway. It shows our work with food chains and the terminology being learned.

***The parents were very interested to know what their child was learning. Several expressed their own frustrations with spelling, and wished they had been taught these things. A few with younger children were hoping that other classrooms were teaching orthography as well.

Just before getting up to leave, one mom turned to me and said, I have something I just have to share with you. I think that because of what you’ve been explaining about orthography tonight, I finally understand a conversation I had with my older daughter (the one that was in my class three years ago).

My daughter and I went round and round a while ago. I was asking her how to spell a word. She said, “What does it mean?”
I said, “I don’t know.”
She said, “I can’t tell you how to spell the word if I don’t know what it means.”
I gave her a surprised look. “What?” I said, “I never knew what words meant. I just memorized how to spell them.”
She looked back at me even more surprised. “That makes no sense! You need to know what it means before you can understand how to spell it!”

That just made my day! Spelling represents meaning. My former student knew that, but her mom didn’t get it until this conference night. I’d say it was a night well spent!

Here’s a final touch. I had this on the whiteboard at the front of my room just in case anyone stopped to take a look.

July 7, 2018 by mrssteven

“Outer Beauty Attracts, but Inner Beauty Captivates.” ~Kate Angell

Like many native English speakers, those who are learning English often express disappointment that words that have identical letter strings do not rhyme (bomb/tomb/comb, read/red, thought/though/through). It’s interesting to me that my own attitude about that has become one of fascinated interest. Where someone else might throw their hands up and cross their eyes, I smile and pause to consider what might be going on with those words. Then I head to a trusted etymological dictionary (usually Online Etymology Dictionary first) to investigate and check out my hypotheses. At times I search through a second or even third etymological resource. Maybe I end up in either my copy of Lewis and Short’s A Latin Dictionary or Liddell and Scott’s Greek-English Lexicon. I might even be led to Richard Venezky’s book, The American Way of Spelling for further understanding. The point is that I will look because I expect there to be an explanation. Those who throw their hands up and cross their eyes have never been taught that an explanation is possible. What a shame. Because an explanation is not on the surface of the word, those people think it doesn’t exist. I guess they’ve never applied the old adage “Never judge a book by its cover” to a word. What a difference that has made for my students and me!

This morning I was reading THIS ARTICLE in Huffpost called “35 Confusing Things About the English Language”. Nine out of the 35 comments listed were related to the expectation that things with similar spellings should be similar in their pronunciations. That’s 1/4 of the comments!

Since I don’t fluently speak another language, I’ve never stopped to wonder whether or not a letter or letter combination in another language is reliably pronounced one certain way. I’ve just always understood that in English it’s not that way. As my respected orthography teacher says, “English spelling represents the language we already speak. Its job is not to teach us how to speak our own language.” The job of English spelling is to represent meaning. You see, words are a combination of morphemes. A morpheme is the smallest functioning unit in the construction of a word’s meaning. As morphemes are joined, the word’s meaning emerges.

A morpheme, either alone or in combination with other morphemes, constructs meaning. Each morpheme on its own might not carry specific meaning, (I’m thinking of a connecting vowel here and perhaps some suffixes) but each has a function in connecting the morphemes that do. In a completed word, every morpheme can be identified, and its function (as it relates to the construction of the word’s meaning) explained. Morphemes are bases (free or bound) and affixes. The base carries the principle meaning in the word. Affixes are either derivational (alter the meaning of the word by building on the base) or inflectional (have a grammatical function). All prefixes are derivational whereas suffixes are either one or the other. Very few people have been taught to look at a word and automatically think about what its morphemes might be and what sense and meaning they bring to the total word. Instead, most people look at a word and think that the spelling of the word dictates its pronunciation. Then they get frustrated that sounding out the letters doesn’t always result in a recognizable pronunciation of the word in question.

I have to wonder if it isn’t our own fault that we have this unrealistic expectation that words spelled similarly must rhyme. After all, think about how we teach reading in our country. Imagine yourself looking in on a primary grade classroom where students are being taught that word families include words that 1) have a certain string of letters and 2) all rhyme. Here’s an example:

What is at the head of this “family”? It is a string of letters that carries absolutely no meaning. After completing worksheets and lessons focusing on many many “families” like this, a student might very well expect that whenever a string of letters seen in one word is also in another, the two words will rhyme. Why wouldn’t they after having it demonstrated to them over and over? Are they ever told that it doesn’t always work that way? Are they ever shown examples of words that share the same string of letters but that DON’T rhyme? Right from the start children are being told something that isn’t always true, only they aren’t told that it isn’t always true. In other words, we are setting them up with this unrealistic expectation. As they begin encountering words for which this is not true, they look to their teachers for explanations. Unfortunately many teachers were never given an explanation themselves, and so have no explanation to share. And boom! The English-spelling-is-crazy-and-makes-no-sense fallacy is born to yet another generation.

What if?

What if we used that idea of a word family to signal something more helpful to a child’s comprehension AND spelling of words. What if we taught children right from the start that a word family is a group of words that share a base, and that a base carries the main sense and meaning found in all words built from that base. And most importantly, that sometimes the base is pronounced the same among words within a family, and sometimes it isn’t. Here’s an example:

The base element here is <sign>, and it has a denotation of “mark”. Now look at all the words I’ve listed that are morphological relatives (that means that they all share the spelling of the base AND they share an ancestor. Their etymological root is Latin signum “identifying mark”. As you think about each of these words, think about their meaning and how it has something to do with making a mark, marking something, indicating something, a symbol, or a designation.

THIS is a word family. There is a meaning relationship and there is a spelling relationship among these words. The meaning relationship is verified by checking an etymological resource to find evidence that they all are from the same root. I found out that the root in this case is Latin signum by looking at Etymonline. I began by searching for <sign>. I know it is a free base (is a word without needing affixes) and found it as both a verb and a noun. Its use as a noun is just a bit older, but both uses were attested in the 13th century. Then I read both entries to find the origin of <sign>. According to Etymonline, other interesting facts about the various uses of this word over time include:

“Ousted native token. Meaning “a mark or device having some special importance” is recorded from late 13c.; that of “a miracle” is from c. 1300. Zodiacal sense in English is from mid-14c. Sense of “characteristic device attached to the front of an inn, shop, etc., to distinguish it from others” is first recorded mid-15c. Meaning “token or signal of some condition” (late 13c.) is behind sign of the times (1520s). In some uses, the word probably is a shortening of ensign. Sign language is recorded from 1847; earlier hand-language (1670s).”

Isn’t it interesting that <sign> became preferred over the use of <token>? When we teach children to check whether two words share a root and therefore a denotation, it is likely they will also learn something about a word’s story (find themselves delving into etymology). They will also have looked at the etymological evidence to see if there is anything that helps explain a word’s spelling. This particular base has had the spelling of <sign> right from the start, but there are other words whose spelling makes sense once we know the word’s origin or influence by languages along its diachronical journey ending in our modern day use.

Teaching children about a word family like this results in them understanding that words have structure. Every word has a base element. We build related words by adding other bases or affixes to the base. Look back at my word web to see how obvious the structure of most of these words is. When we teach children about a word’s structure, we are teaching them about a word’s morphology. Announcing word sums is a way to reinforce our understanding of word structure. Take <designate>. The word sum is <de + sign + ate –> designate>. It would be announced as “d e plus s i g n plus a t e is rewritten as de sign ate.” The elements are spelled out, the arrow is announced with “is rewritten as”, and when spelling the finished word there is a slight pause between the elements to show recognition of those boundaries.

The third major consideration in teaching children about a word family as I have described it is that pronunciation piece. Studying a word family teaches children the reality about whether a common string of letters will always rhyme. It won’t. And with this kind of word family representation, they won’t ever think it should or be surprised that it doesn’t. As an example, let’s look at the family for <sign>. When we pronounce <sign>, <signer>, <cosign>, and <assignment>, the base is pronounced [saɪn]. But what happens when we pronounce <design> and <resign>? The base is pronounced [zaɪn]. And when we pronounce <signal>, <signify>, and <signet>, the base is pronounced [sɪgn]. In these three words the <g> is pronounced. But it isn’t pronounced in eight of the family members I’ve included in this web!

Just think about that. If spelling were there so we knew how to pronounce a word, most of the words in that one family would have different spellings. But they don’t! They are spelled the way they are to represent the meaning that they all share! The meaning and the shared spelling is what binds these words together into a family. We don’t have to blame the English language because words that look like they might rhyme don’t. Instead we need to appreciate the fact that the unpronounced <g> in this family is an allophone of /g/, and its presence marks a meaning connection to members of this family in which it is pronounced. Pronunciation is not consistent enough to be the reason for a word’s spelling, but a word’s sense and meaning is!

You may be thinking that <sign> is a word that would not be studied in a primary classroom. But why not? Surely the children know some of its related words. They don’t need to be able to read the words to understand that they all have <sign> in their spelling. They can talk about what the words mean and the teacher can talk about the structure, meaning, and even point out the differences in pronunciations of the base. More of the students will understand this than you might think, and the rest will be gaining a foundation for a more accurate understanding of how our spelling system actually works. Any classroom should make it a point to look at words that interest the students no matter how many letters the word has! If the focus is always on the structure, the meaning, the word’s relatives, and the interesting things to note about the word’s grapheme/phoneme relationships, then the word is the vehicle for the understanding. Perhaps have an “I Pick – You Pick” philosophy for choosing words to look at. It will really drum up interest!

Look at this word web that is centered around <dog>. As you include more and more of these, you can start the discussion with, “What do you notice?”

It will not take long before students say things like, “I see the word <house> in <doghouse>”. Then you know it’s time to talk about compound words. This word web could also lead to a discussion about the final pluralizing <s>. Maybe your students could quickly help you make a list of plural words and you could write them in two columns: those in which the final grapheme <s> is represented by /s/, and those in which it is represented by /z/. It won’t be long after that before they will be pointing that very thing out in plural words they are reading! And then there is the doubled <g> in <doggy>. It is not too early to talk about the doubling convention that happens when we add a vowel suffix to a base. Explain it and talk about it as an interesting thing to notice. Say something like, “I think I’ve seen that in the word <scrubbing> as well. Keep your eyes open. If you see a word that you think has a doubled consonant because of a suffix being added, let me know, and we’ll look at it together!”

Here’s another great tip: Don’t put a word web like this away until you have given students a chance to think of other words that might belong to this family. It will give you the opportunity to see what kinds of connections they are making. What if they suggested ‘hot dog’? Instead of responding yourself, give the other students the opportunity to respond. “What do the rest of you think? Does it belong? Why or why not?”.

This kind of word family is the only kind of word family. You can still talk about rhyming words if you want, but don’t call them families. If you are using them to help a child read, begin incorporating true word families as I have suggested. Sometimes we decide what our students can and cannot handle. Sometimes we misjudge them. If you are hesitant to study word families, your students will be the ones to convince you otherwise. When they point out something as they are reading in class, when they bring in a word web they made on their own at home, when they explain a suffixing convention you have previously explained, or even when they ask a question about a suffix that you didn’t expect them to, you will know they are on their way to building an understanding about the reliability of our spelling system. And you can feel great knowing that the group leaving your classroom has been taught to see below the surface of the word. They’ve peeked beneath the cover and are now judging a word by its structure (morphology), story (etymology), and grapheme/phoneme correspondences (phonology). And they are captivated!

************
I encourage you to click on the comments. The link is just below the end of this post in small letters. Peter Bowers has written a great response and has included links to research that may be of interest. Like I said, check it out!

May 21, 2018 by mrssteven

“Stop Learning and Start Thinking”

I shared this video with my students the other day. It is about 7 years old, but its message is timeless and crucial if we are to teach our students how to be in charge of understanding their world. The boy speaking is Jacob Barnett. At the time this video was made he was 11 years old. At present he is 19. If you have not seen this, please watch it now. It is 18 minutes long, but well worth your time. If you have seen it before, watch it again. Having Jacob’s voice in your head as you continue to read this post will give strength to what you read.

When it was over, I said, “Well, What do you think about what he said?” One student mentioned how smart Jacob is. Another said it was weird that Jacob wore sandals. Another commented that he could tell Jacob was “different”. Yet another noticed that he had the Greek letter phi (φ ) on his shirt. (We’ve been learning the Greek alphabet). It got kind of quiet after that. So I said, “What do you think Jacob means when he says you have to stop learning and start thinking?” Now it was completely silent. And the silence was paired with facial expressions that said, “I don’t have any idea what that could mean!”

At that point I shared my own thoughts: When Jacob says to stop learning, I think he is talking about learning as it is typically done in schools. You know how it goes – the teacher tells the students what he/she wants them to know. They learn it. (This might include reading about it, writing about it, watching videos, etc.) Then the students take an assessment to see how well they learned it.

THAT is what Jacob wasn’t able to do when he was young – because of his learning differences. THAT is what Sir Isaac Newton wasn’t able to do when attending the University of Cambridge – because the school was shut down with the outbreak of the plague. And THAT is what Albert Einstein wasn’t able to do – because he was Jewish and turned away from the local university, so he ended up taking a job working in a patent office instead.

Each was prevented from following this model of learning, and in doing so, had time to think. Jacob believes it was this time to think and question and seek understanding that lead each person to their discoveries. Now, does this mean Jacob didn’t learn things by reading books? Of course not. When he had posed questions that he wished to explore and knew more information was necessary to move forward in his thinking, he read the books he needed to read! In other words, he read books and focused on understanding what he was reading. He was a motivated reader. The information he learned while reading helped him formulate new questions and better understand whether or not his past questions were on the right track. In this manner he was always motivated to deeply understand a specific topic in order to weigh whatever questions he was currently posing.

So did he in fact “stop learning”? I don’t think so. I think he stopped being a passive participant in learning, and became an active one. And he found his inner voice – that unique perspective that he has – that each of us has with which to do our thinking. Jacob explored the questions he had in a way that came natural to him. Unfortunately, the way schools are set up, students often lose sight of their own unique perspective as they get older. They get used to waiting for an adult to tell them what to do next, what information to search for, what answer to find. They become passive learners. And as passive learners, they rarely go beyond what has been laid out as the expectations for a particular assignment. If doing “a, b, and c” is what is required, very few will ask about “d”. Sometimes teachers will comment that there are students who are capable of doing more, but lack motivation. Do they really lack motivation, or have they become passive? Are YOU sometimes a passive learner?

At this point Ella raised her hand. “When we study words, we’re not passive. It’s like how Jacob learns. We do a lot of thinking about what the word means, and then we come up with a hypothesis for our word sum. We read whatever dictionary we need to while collecting our evidence and the word’s story. But WE do it ourselves.”

I answered, “Yes! You work independently and are actively involved in your learning! You look at resource books when you need to. You search for evidence to support or disprove your word sum hypothesis. You discuss with others what you are thinking about as you are finding information and hypothesizing. And often another person’s unique perspective helps you stretch your own thinking. You research and investigate and gather your evidence until you’re satisfied you understand as much as there is to understand at this time! The best part is that you recognize that you have not found an answer. You have found a temporary understanding that may in fact deepen should other evidence come to light!”

Ella continued rather proudly, “When we were taking the Forward Exam a few weeks ago, I was trying to think of what the word sum would be for <conversation>. I knew about the two possible suffixes <ate> and <ion> on this word which left <convers(e)>. I also recognized the prefix <con>, although I couldn’t remember what it meant just then. That left <vers(e)>. When I thought about that, I thought of how a verse is something I read, write, or talk about. A conversation is talking between at least two people, so I knew I was on the right track. I couldn’t look it up during the exam, but later I checked it out to see if what I thought made sense.”

I was not expecting Ella to point out this correlation between what Jacob was describing and what we do in class, but I was delighted she did! The students can FEEL the difference between passive and active learning. They recognize their own level of engagement, and how using a scientific lens to look at words has drawn them in and increased their level of interest. The fact that Ella shared her thinking about the word <conversation> and how being able to do that helped her in a situation outside of class, proves that Structured Word Inquiry has become the way she thinks about words! Ella KNOWS that a word’s spelling is not random. She KNOWS to expect its structure to make sense and to help her understand the meaning of that word.

I remember what a former student said at the end of her fifth grade year, “In fourth grade we had a list of words. We wrote them on our white board over and over again until we could spell them without looking. It got very boring very quickly. In fifth grade it’s different. We investigate a word to find out where it comes from, and what it’s word sum might look like. We find out its history and how it’s been used. Then we write about what we found, and after we’ve collected words with the same base we make a matrix. It’s a lot more work, but it is also a lot more fun!”

Did you hear that? It was a lot more work, but it was also a lot more fun! We have to stop deciding what is too much work or what is too hard for our students. We have to stop simplifying tasks to the point of rendering them uninteresting and requiring too little thought.

Structured Word Inquiry versus the Scientific Method

What my students do with spelling is not much different than what they do in preparation for our Science Fair. The first step is to choose a topic or a word. Next they do a bit of research. For both spelling and science, they need to know enough about their topic to create a thoughtful hypothesis. Let’s say a student is curious about the effects of music on a person’s heart rate. Before writing a hypothesis, that student would benefit from finding out what a typical resting heart rate is. It might even be helpful to find out what is considered to be an elevated heart rate. The student might also want to know how many beats per minute specific music has. The student’s hypothesis can include those pieces of information, and later on, the data collected can be compared to that hypothesis. The student investigating a word will want to brainstorm a few other words related to the targeted word. Which structural pieces are the same? Which structural pieces are different? I am speaking of morphemes. Does the student recognize affixes that could be removed in order to identify the base or bases? A hypothesis in this situation means a possible word sum. Oftentimes a student will consider two or three different word sum hypotheses.

The next step in either scenario is to research deeply. The person preparing a science experiment will want to find out more about music types, heart rates, the effects music has on people, and maybe even music therapy. The person investigating a word will want to find out when his/her word was first attested and what it meant at that time. The person may consult several etymological references to find out the word’s language of origin and its spelling in that language. What was the lexical stem in that language of origin that became today’s base element? In the process, the word’s story is revealed. It may have meant different things at different times in history. It may have had its spelling changed (for a variety of reasons) by the different groups of people who used it over time.

Now it is time for the scientist to set up the experiment, run it, and collect the data. This will take some time. The person running the science experiment will select a group of people to participate. Resting heart rates will be taken, and then music will be played. Then heart rates will be taken again. There will be tests for different kinds of music, and the group of participants will be tested several times for each type of music. The student investigating a word will now focus on collecting words that share the word’s root (ancestor) which was found during research. Words found that share both the word’s ancestor AND the base’s spelling are listed as morphological relatives. Words found that share the word’s ancestor but NOT the base’s spelling are listed as etymological relatives. In both cases it is important to keep a journal detailing this collection process in case the experiment gets repeated at a future time.

The data is collected. What’s next? The student who is preparing for the Science Fair will begin making graphs and/or charts of the data so this person can make observations. After careful consideration of what the data shows, the student draws some conclusions. Does the data support the initial hypothesis or does it falsify it? At this point, either outcome is valid. The student learns about the effects of different types of music on a person’s heart rate regardless of whether or not their hypothesis was “right”. Proving the hypothesis is what drives the experiment, but if the hypothesis isn’t proven, the experiment has not failed. It has only moved the student in a different direction with their questions and thinking. In so many respects it is the same for the student investigating a word. This student looks at the morphological relatives found (the words that share a common ancestor AND the base element’s spelling) and writes those words as word sums. As the student does this, special attention is paid to the the morpheme boundaries. This is where the student’s understanding of the single final non-syllabic <e> as well as suffixing conventions come into play. For example, let’s say the student was writing a word sum for <describing>. If the student wrote the word sum as <de + scribe + ing –> describing>, I would know that the student understands the importance of the single final non-syllabic <e>. The <e> is part of the base element in this word. If it wasn’t, then adding the vowel suffix (<-ing>) would force the (then) final on the base to double. The student includes the <e> on the base element to prevent doubling! When the words are all written as word sums, a matrix is created. (Just as there are several kinds of graphs on which to display science data, there are other ways to present word collections as well. A matrix is the one to use when looking at all the elements – affixes and other bases – that can be used with a common base.)

Once the graphs/matrices are made and the students have made a list of observations, it is time to share their findings with a larger group. The student who is presenting at the Science Fair will pull out the journal with the detailed notes and type up a list of procedures, some of the research findings, the hypothesis, the observations and more. Those will be displayed along with the graphs or charts and any pictures on a display board. The student doing the word investigation will decide whether to create a poster, a booklet, a skit type presentation, a video, or some type of digital presentation (perhaps similar to Powerpoint). This person will also go back to their journal with the detailed notes and share the word’s meaning, the attestation date, the language of origin, and other interesting things that were found out about the word’s history. They will also share the matrix they created, the related words, and any observations they have made as they reflected on their investigation. For instance, they may have noticed interesting things about the phonology in this word’s family. Perhaps this word is Hellenic and has a <ph> grapheme that represents a /f/ phoneme. Perhaps there are pronunciation differences in the base of the word family as there is in the family that includes predict, diction, and indictment. The students usually include the word in IPA so they can specifically talk about the grapheme/phoneme relationships.

As each student presents, they walk us through their exploration. They share the most surprising things they found out and ask for questions. Their explorations, whether the kind shared at a Science Fair or the kind shared with fellow word enthusiasts in a classroom, always get great interaction from the audience. The work investigated with this scientific lens is so worthy that audience members can’t help but become engaged themselves and think of their own questions.

It sounds like a lot of work doesn’t it? I bet some of you are even thinking, “My students can’t do all that.” But given the chance, your students will prove to you that they can. My students begin fifth grade with very little true understanding about our written language. But amazingly, within two to three months of school they are eager to investigate words on their own and in much this way! They are so hungry to be actively involved in their learning! As we continue through the year, they become more and more independent in their pursuit. THIS is what Ella was pointing at when she said that our word work was a lot like what Jacob Barnett was describing. When we investigate words (and conduct science experiments), we “STOP LEARNING AND START THINKING“!

May 5, 2018 by mrssteven

Guess What? They’re ALL Silent Letters!

I found an article the other day that made me kind of sad. The article was posted online by the Oxford Dictionaries and was called, “Why English is so hard to learn: silent letters.” Here is a link to the article. The first thing that struck me was the term “silent letters”. I am aware that letters that are unpronounced in a word are commonly referred to as silent letters, but that doesn’t make it accurate. I also admit that in the not too distant past I called them that as well … because that was what I was told they were. In a world where children are taught that letters routinely “say” sounds, as in the letter f says /f/, it might indeed seem to make sense to call the <g> in <sign> silent since it isn’t “saying” anything.

But I’ve come to realize how misleading that way of thinking is. And it is. Very misleading.

Letters produce sound?

Let’s begin with the underlying assumption here that letters do make sounds. Obviously they do not. Can not. They’re just symbols printed on paper. Yet we ask children to believe that they do. In fact we begin a child’s reading instruction by teaching them that the consonants each “make” one sound and the vowels each “make” two. What we really mean here, and what we should really be saying to children is that graphemes represent pronunciation. (Graphemes are letters or combinations of letters that represent phonemes.) So for example, we can say that the grapheme <s> represents /s/. But don’t stop there. If you don’t want to get into all of the pronunciations that the grapheme <s> CAN represent, then just say, “The grapheme <s> CAN represent /s/. It can also represent other pronunciations, but right now we’ll focus on /s/.” Using this wording leaves the door open to other pronunciations of the grapheme <s> as they will, without any doubt, notice in words. The students won’t be gobsmacked when it happens. They will have been waiting for it and looking forward to understanding why and when <s> has other pronunciations.

With this slight change in OUR explanation, we are switching from having children think something is possible (that even THEY can recognize is not) to simply stating the truth. Changing your wording may seem trivial to you as you are reading this, but within a year or two of learning to read and write, children are already beginning to see our language as one that makes no sense. And the fact that the adults don’t understand our language as well as they could, doesn’t help. Many just repeat what they were taught or what some teacher manual says to repeat. They don’t question what they don’t understand because their own education regarding our language has unintentionally taught them to believe that our language makes no sense. I imagine that you have seen the same kinds of “proof” that I have where someone asks about house and mouse, and that if the plural of mouse is mice, why isn’t the plural of house hice? There are lots of those kinds of questions offered up as proof that English spelling cannot be understood. And perhaps, if the only aspect of English spelling that has been presented is that of the “sounds” of letters and words, then of course it might feel impossible to understand.

Learning grapheme, digraph, and trigraph pronunciations in isolation?

Can you imagine teaching children to read music by holding up a card with a musical note drawn on it and expecting them to sing it? Of course that wouldn’t work because until they see the note on the proper line of the musical staff, or hear it in comparison to the note in front of it or behind it within a song, they won’t know the right note to sing. Expecting children to recognize and accurately sing all of the notes before they see any of them on a staff or in a measure of music is ludicrous. Before children learn to read music, they have sung hundreds of songs. They have sung the notes in hundreds of combinations. But not in isolation. Each note makes sense in its setting, in the context of its song.

Is it so different with children who are learning to read? Why don’t we teach them graphemes, digraphs, and trigraphs in the context of a word or even a sentence? Because THAT’S where those pronunciations become clear and predictable. Perhaps begin with a word that is used in a story you are reading. The child can get a feel for how the word is used and what it means by pulling it out of context for a closer look. Maybe you’ll want to think of other words related to this one. For example, if you are focusing on the word ‘dog’, maybe you want to talk about a dog house or dog food or dogs. You can both count how many letters are in the word. Then point out that each letter in this word represents a grapheme, and that each of those graphemes represents a phoneme. Then pronounce each. You might point out that in any word that has a final <g>, that <g> will be pronounced /g/. Then you can brainstorm some other words with a final /g/. Then again, maybe the student wants to pick out a word to look at. Maybe it could be routine that every time you read a story together, you each pick out a word to look at and think about. Review the names of the letters and compare the way graphemes are pronounced in words. For example, compare the <s> in small to the <s> in dogs. Find some other words with a final <s> and practice reading the words together and feeling whether the final <s> in those words is pronounced /z/ or /s/. This might even be that opportunity to find graphemes in words that are unpronounced!

It is common practice to teach graphemes and digraphs in isolation. I remember back a bunch of years. Our spelling list included words in which the main vowel was called “long e” and pronounced as /i/. The students would brainstorm different letter strings we could use to represent that pronunciation. We came up with <ee> as in reel, <ea> as in read, <ei> as in received, <ie> as in chief, <e> as in be, <y> as the final letter in baby, and <e_e> as in these. Every week we would brainstorm these patterns and then think of words that used those spellings for that pronunciation. What busy work! The students would ask, “How do you know which of those spellings is in a particular word?” I couldn’t answer because I didn’t know. After a while they stopped asking and they resigned themselves to empty memorization. What I was doing didn’t make them better spellers unless they were already great at memorizing. You see, looking at the vowel pronunciation and all the letter strings that might represent it just made matching them up feel very random. To the students, it was like playing “take a guess.”

It makes much more sense to start with a word that a student has come across and that they are interested in.

So why are some letters in some words unpronounced?

Let’s focus on some of the letters identified as “silent” in the article. We’ll look through a few at a time so I can explain some possible reasons for that letter not being pronounced in that word.

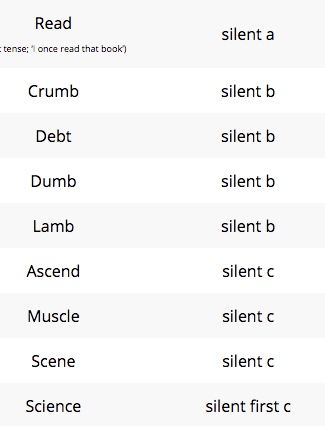
Let’s begin with read, as in “She read that book yesterday.” The <a> cannot be considered unpronounced because it is not functioning independently in this word. It is part of the digraph <ea>. That means that the two letters are representing one grapheme which is representing one phoneme. In this word, the digraph <ea> is representing /ɛ/ as it does in bread, feather, and breath. This digraph can also represent /i/ as it does in team, eat, and bean. The fact that this one digraph can be representing two different phonemes makes it perfect for this word. If you look at other words in this family, you’ll see that both of these pronunciations are present: <ea> as /i/ – read, reading, readable, reader, readability, readership, misread, and <ea> as /ɛ/ well-read, read, misread. The meaning of this base is constant, but the pronunciation of the base is dependent on the context in which we find it, as well as the affixes attached to it.

The next word on the list is crumb. The in this word is considered a marker letter. It is marking its connection to other members in its family in which the IS pronounced. That would include words like crumble, crumbling, and crumbled. If the were removed from <crumb> just because it is no longer pronounced, we would not recognize this word as belonging to this word family and sharing its meaning.

Since dumb and lamb have a similar placement of , let’s look at them together. These two have a similar story. The final in both of these words marks their etymological origins. The word dumb is from the Old English word dumb. At that time it meant “silent, unable to speak”. Even though it has come to mean other things as well, its spelling has not changed. The word lamb has a story that is not very different. It is from the Old English word which was spelled either as lamb, lomb, or lemb depending on where one lived. In both dumb and lamb, the final has been there from the beginning. And even though we don’t pronounce it, it is part of this word’s identity. When we see words like lambskin, lambkin, and lambswool, we instantly know these are related to the animal we know as a lamb.

In Modern English spelling, the consonant cluster <mb>, when found final in a word, is considered to be unpronounceable. In that case, the last letter in the word is unpronounced. This explains why we don’t pronounce the final in crumb, dumb, lamb, tomb, bomb, and thumb, yet we DO pronounce that in related words like thimble, crumble, bombard, and rhombus.

The word debt has a very interesting story to tell. It’s etymological journey begins in Latin with debitum “thing owed.” Its spelling changed for a while because of a French influence (dette, dete). Sometime after c.1400, the was restored. So once again, this unpronounced grapheme marks a connection to this word’s root. It is interesting to note that the IS pronounced in the related word debit where we see the two graphemes separated by a vowel.

Next up is ascend. This word is from Latin ascendere “to climb up, mount.” The <c> would have been pronounced /k/ in Latin. When we compare it to descend, we can hypothesize that the base element is <scend>. The prefix is an assimilated form of <ad-> “to, near, at”. The Etymonline entry for this prefix states that the <ad-> is simplified to <a-> before an <sc>. That gives us information about the word’s structure, but not the pronunciation (or lack thereof) of the <c>.

In thinking about the <c> here, I wondered whether or not it IS pronounced in words in which it appears to be paired up with the <s>. I went to Word Searcher and found a long list of words with an <sc> letter string. Here are a few of them: scone, scope, scoot, scrub, screw, scab, scale, scarf, scream, and rescue. I also noticed other words in which the <c> seemed to be unpronounced. Here are a few of them: descent, scion, scenic, scent, obscene, scepter, scissor, and scythe. In looking at the lists it became obvious to me that this is just a case of knowing the pronunciations that can be represented by the grapheme <c> and what governs that. When followed by an <e>, , or <y>, it will be /s/. When followed by anything else, it will be /k/. When the <s> AND <c> in a word would both be representing /s/, they function instead as a digraph representing a single /s/.

Two other words in this list have the <sc> pronounced as /s/. The first is scene. This word originated in Greek as σκηνικός “of the stage, scenic, theatrical.” It is transcribed as skenikos. When the Greek suffixal construction <-ikos> was removed and this word was transcribed into Latin, the <k>’s were written as <c> (scene), but the pronunciation of the <c> remained /k/. As had happened in many many instances, this word was influenced by Middle French speakers (scéne) and the <c> lost its hard pronunciation. Today we can recognize the <sc> as a digraph representing /s/.

The last word in this group is science. This word is from Latin scientia “what is known, acquired by study.” If we further analyze this word, we find the base element of <sci> “know, be able to separate one thing from another.” It’s the same base we see in conscience, unconscious, and conscientious. Do you see the meaning connections there? Isn’t that fascinating? A tangent, I know, but sometimes I can’t help it! Back to the phonology of the <c> in science. In Latin, the <c> would have been pronounced as /k/, but like scene, as this word journeyed through time, it was influenced by French speakers – (Old French science). The <c> took on a /s/ pronunciation which persists today.

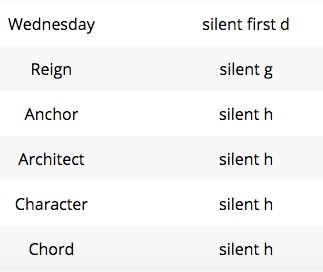
It’s time to look at Wednesday. This day of the week was originally named for the Roman god that corresponded to the planet Mercury. That is why the Romance languages (French, Italian, Spanish, etc.) spell this day as Mercredi, Mercoledi, and Miércoles respectively. When the Germanic people adopted this naming of the days, they switched out the Roman gods for their own gods who had similar characteristics. The day known as Dies Mercurii to the Romans became known as Woden’s Day to the Germanic people. Can you see now how Woden’s Day became Wednesday? There is a slight difference with the letters which no doubt prompted the <d> to lose its pronunciation. Once the <en> in Woden was reversed and the <o> changed to an <e>, the <dn> letter string became less pronounceable. If you say the word ‘Wednesday’ several times, you can feel the elision happening and the <d> becoming unpronounced.

Next up is reign. The Etymonline entry shows that the verb form of this word is from Latin regnare “be king, rule.” Moving forward through time, this word was adopted and adapted in Old French where it was spelled regner. In its noun form it gained the and was spelled reigne. Seeing that the <gn> has always been part of this word’s spelling, I looked for relatives of this word to see if the <g> is pronounced in any of those. I found the words regnant “reigning, exercising authority” and regnal “pertaining to a reign.” So it seems that in Modern English the <g> is pronounced when the base is <regn>, but not pronounced when the base is <reign>.

Next on the list is anchor and what an entertaining story awaits! The Etymonline entry lists this word as beginning in Latin as ancora “an anchor.” The information there also points to the Greek ankyra “an anchor, a hook” as being either an earlier ancestor or perhaps a cognate (emerging at the same time). This information is especially interesting because of the Greek letter kappa being transcribed to the Latin <c>. A modern English <ch> spelling that is pronounced as /k/ usually originates from the Greek letter χ (chi) which was transcribed into Latin as <ch>. That did not happen here. So why is the <ch> representing /k/ in this word?

Reading on at Etymonline, the story is revealed. The <ch> is NOT etymological and was inserted in the late 16th century, “a pedantic imitation of a corrupt spelling of the Latin word.” So even though the <ch> in this word is NOT derived from the Greek letter chi, it now looks like and behaves like it was, including being pronounced /k/. The <h> is part of the <ch> digraph. It is not operating as an independent grapheme.

So what about architect, character, and chord? They each have <ch> representing /k/. Do they share a Hellenic ancestry? Well, architect is from the Greek αρχι-τέκτων “chief builder.” That would have been transcribed by the Romans as archi-tecton. As you will notice, the third Greek letter was χ (chi). When that letter was transcribed by the Romans, they transcribed it as <ch> and pronounced it /k/.

Digging into the etymology of character we find that it is from the Greek χαρακτήρ “engraved mark”. As you can see, the initial letter in Greek was again χ (chi). This word was transcribed by the Romans as character . The initial <ch> was pronounced /k/. This word lost that <ch> spelling for a while. At one point it was adopted and adapted by Old French and its spelling changed to caratere “feature, character”. It was sometime in the 1500’s that the <ch> spelling was restored.

So what about chord? Will we see that it too has a <ch> that derived from the Greek letter χ? Prepare for another interesting word story! This word has two entries. The first is as a noun meaning “two or more musical notes sounded together”, and is from 1608. It is an alteration of Middle English cord, a shortened form of accord. The second is as a noun meaning “a structure of the body, emotions figuratively considered as a string on a musical instrument, straight line connecting two points on a circumference”, and is from 1543. The note of interest is this statement in the Chambers Dictionary of Etymology: “English chord(2) and Latin chorda, both meaning a string of a musical instrument have influenced this word by association of form and meaning.” If the Latin word was chorda, that initial <ch> is like the others we encountered in character and architect. It was originally a χ (chi) in Greek. The Greek word was χορδή “a string of gut, the string or chord of a lyre or harp.”

So what about the claim that in the words anchor, architect, character, and chord the <h> is silent (unpronounced)? It is not. The <h> is part of the digraph <ch> that represents /k/ in these words. When you see this particular digraph representing /k/ in a word, it is usually marking a Hellenic heritage.

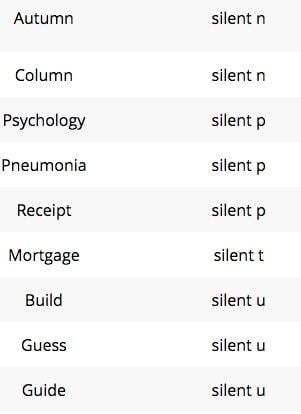
The words autumn and column have a final <n> that is not pronounced. Why? When we look at autumn we see it is from Latin autumnus. Minus the Latin suffix, the spelling is a direct derivation. Interesting side note: This season was called Harvest by the English until Autumn displaced it in the 16th century.

The word column is from Latin columna “pillar.” Again, the Modern English spelling is a direct derivation. The final <n>’s in these words may not be pronounced, but they are pronounced in other members of these word families. Think of autumnal, autumnally, columnist, columnar, columniation. We can think of the final <n> marking a connection to its relatives!

The word psychology takes us back to Greek. How do I know? Check out the <ch> grapheme representing the phoneme /k/! But with this word we are to focus on the initial <ps> cluster in this word. This word was coined in the 1650’s from a Latinized form of ψυχικός “breath, spirit, soul.” You see and recognize the third letter in, right? It’s χ (chi). It was transcribed by the Romans as <ch> since they didn’t have a letter that was its equal. Well, look at the first Greek letter in the same Greek word. It is the letter ψ (psi). When it was transcribed into Latin, the Romans had no equivalent letter, and so transcribed it as <ps>. In Modern English, this cluster is considered unpronounceable when it is initial in a word. We pronounce only the <s> in words like psychiatrist and psychedelic. Both the and the <s> are pronounced though, in words like biopsy, autopsy, and epilepsy.

Next on the list is pneumonia, and the focus is on the initial unpronounced . This word comes from the Greek word πνεύμων transcribed as pneumon “lung.” The reason we no longer pronounce the inital is because of its placement. Richard Venezky (The American Way of Spelling) describes this cluster as unpronounceable when it is initial. When we see this cluster in another position, that is not the case. Look at apnea and tachypnea.

Now let’s look at receipt. The focus here is also the unpronounced . This word is from Old French recete and before that from Latin recepta “received.” According to Chambers Dictionary of Etymology, “The English spelling with p (in imitation of the Latin form) is first recorded in the late 1300’s, but did not become the established form until the 1700’s.” So the was in the spelling of the Latin word recepta, but disappeared as this word was adopted and adapted in Old French. It reappeared sometime in the late 1300’s, and became part of the established form of the word in the 1700’s. That explains its place in the word, but what about it not being pronounced? Well, according to Richard Venezky, there are a small group of “borrowings and scribal tamperings” in which the is unpronounced. Besides receipt, examples include corps and coup.

With mortgage we’ll be looking at the unpronounced <t>. According to Etymonline, this word was first attested in the late 14th century as Old French morgage “conveyance of property as security for a loan or agreement.” This Old French word is from mort “dead” and gage “pledge”. This name is fitting because “the deal dies either when the debt is paid or when the payment fails.” Old French mort is from Latin mortuus. The <t> was not evident in the Old French word, but was restored in English based on the Latin. This word is considered a French borrowing with the <t> restored to mark an etymological connection to its Latin root mortuus. As such, the <t> is not pronounced.

The next three words have unpronounced ’s. The first is build. It is from Middle English bilden and earlier (probably 1200) it was bulden “dwelling.” According to Chambers, “It was not until the late 1500’s that our spelling begins to appear with frequency. Even so, the spelling is not accounted for, unless it is simply a composite of the two earlier spellings bilden and bulden.” The sense and meaning of putting something together came about in 1667. Although is found in words like guild, guilt, guitar, and circuit, and therefore might appear to be a <ui> vowel digraph, it is not. The has a specific function in those words that it is not performing in build. I will explain further in the next paragraph as we look at the words guess and guide. In the word build, the is unpronounced.

The word guess is from Old English gessen “infer, perceive, find out.” According to Etymonline, the <gu> was late 16th century. This sometimes happened in Middle English to signal a “hard” pronunciation of the <g>. In this word, the unpronounced is considered a marker letter. It marks the pronunciation of the <g>.

The last word in this group is guide. This word is from Old French guider “to lead, conduct.” The has always been part of the spelling of this word. Here, the unpronounced is considered a marker letter as it was in guess. It is marking the “hard” pronunciation of the <g>.

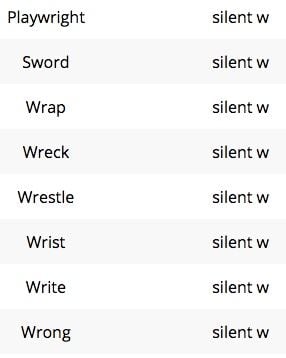
This last group of words are all listed as have a silent w. Let’s find out what we can about them.

First up is playwright. According to Wikipedia, “It appears to have been first used in a pejorative sense by Ben Jonson in 1853 to suggest a mere tradesman fashioning works for the theatre. Jonson described himself as a poet, not a playwright, since plays during that time were written in meter and so were regarded as the province of poets.” You see, at the time, the word wright was Old English wryhta, wrihta “worker.” Ben Jonson saw what he did as above the rank of a worker. He referred to himself as a poet and not a playwright.

As far as the <wr> spelling, Etymonline notes that it was a common Germanic consonantal combination (and that we can see for ourselves when we look at the Old English spelling). It is especially interesting to note that the <wr> combination often starts words that imply twisting or distortion. A worker or crafter might indeed need to twist in order to craft something! Etymonline goes on to note that the <w> ceased to be pronounced sometime c. 1450-1700.

The next word on the list is sword. This word is from Old English sweord, swyrd, sword “cutting weapon.” As you can see, the <w> has been part of its spelling since its beginning and was no doubt pronounced at that time. Even though that <w> is generally unpronounced in this word, we can consider the <w> as marking its language of origin.

Now let’s look at wrap. This word was first attested in the 14 c. as Old English wrappen “to wind something around something else.” This is the same common Germanic consonantal combination we saw in wright that starts words that imply twisting or distortion. To wind something is certainly to twist it!

Wreck was first attested in the early 13th century, “goods cast ashore after a shipwreck.” Before that it was from Anglo-French wrec and before that from a Scandinavian source. A note of interest here from Etymonline is that “wrack, wreck, rack, and wretch were utterly tangled in spelling and somewhat in sense in Middle and early modern English.” And, again we see that same Germanic consonant pair <wr> that can imply twisting or distortion when initial in a word!

I bet you already see the Germanic consonantal combination in wrestle and can see the implication of twisting and distortion in this word’s meaning. This word has a frequentative suffix <-le>, which means the action happens over and over. The base wrest is from Old English wræstan “to twist, wrench.” Once again, the <w> may no longer be pronounced, but it is marking that etymological connection to Old English and the <wr> combination here implies twisting and distortion.

Next up is wrist. I bet YOU could tell ME about that <w> this time! Yes, it IS from Old English. It was spelled wrist and the notion was “the turning joint.” In other words, the <w> is unpronounced and marks the etymological connection to its Old English roots and the <wr> combination here implies twisting and distortion.

Now let’s look at write. It is from Old English writan “to score, outline, draw the figure of.” Once again we have the <w> marking its connection to its language of origin, Old English, and that <wr> implying twisting and distortion.

The very last word on the list is wrong. Surely this word will have a different story to tell. Let’s see. It’s from late Old English “twisted, crooked, wry.” According to Etymonline, “the sense of not right, bad, immoral, or unjust was developed by c. 1300. Wrong thus is etymologically a negative of right, which is from Latin rectus, literally straight.” You will recognize the Latinate base <rect> in the word correct! As for the <w>? It functions just like the <w> in playwright, wrap, wreck, wrestle, wrist, and write. It marks the connection to the Old English heritage each word has. And when paired with <r> in words of Germanic heritage, an initial <wr> often implies a twisting and distortion of some sort.

Here’s a list of the words once more with an explanation for the unpronounced letter in each:

read … the <a> is part of the digraph <ea> and as such is not an independent letter in this word.
crumb … the marks a connection to other members of the word family in which it is pronounced, such as crumble and crumbling.
debt … the marks a connection to the word’s root and related words in which the is pronounced, such as debit.
lamb, dumb … in Modern English, the <mb> is considered an unpronounceable cluster and as such the final letter is unpronounced.
ascend, scene, science … the <sc> represents /s/, so the <c> is part of a digraph.
Wednesday … the <d> followed by an <n> caused the <d> to be elided (unpronounced).
reign … the <g> is unpronounced but marks a meaning connection to a related base <regn>.
anchor, architect, character, chord … the <h> is part of the <ch> digraph representing /k/ which signals a Hellenic heritage.
autumn, column … the <n> marks a connection to other members of the word’s family in which it is pronounced, such as autumnal and columnist.
psychology … the <ps> marks a Hellenic heritage. When the <ps> is initial, the is unpronounced.
pneumonia … when the <pn> cluster is initial, the is unpronounced.
receipt … the is unpronounced in this word as well as in corps. It is part of a small group of “borrowings and scribal tamperings” that have unpronounced letters.
mortgage … the <t> marks the historical language of origin (Latin) of <mort>.
build … the is unpronounced and although there are ideas about the historical phonology, I could not find an agreed-upon explanation.
guess, guide … the marks the “hard” pronunciation of the <g>.
sword … the <w> marks the language of origin (Old English) and a time when the <w> was pronounced.
playwright, wrap, wreck, wrestle, wrist, write, wrong … the <w> is part of the Germanic <wr> consonant cluster that implies twisting and distortion.

Labeling letters as silent is a problem.

The problem with calling a letter silent is that it feels like an explanation to someone who is learning to read. “Oh. Don’t worry about the <g> in sign. It’s a silent letter. Just skip over it.” That learner will probably become as complacent as the adults around him and not even look for an understanding as to WHY it is not pronounced in that word. And, of course, by just moving on, thinking there is no reason for it to be there, they will miss out on understanding a whole lot about digraphs, markers, etymology, word families, and phonology.

Just imagine what it would be like if letters COULD talk. What if they could each tell you their history or how pairing them up with other letters to form graphemes matters! What if they could tell you that their coming together in a spelling is like music and the melody each word creates is in their sense and meaning!

Until then, let’s speak on their behalf. Let’s not lump all unpronounced letters into one mislabeled group. Unpronounced does not mean uninteresting or without purpose. Let’s celebrate the history and individual awesomeness of each!

So what is the truth here? Are these letters silent? Sure they are. But then again, so is every other letter in the alphabet. A better attitude to instill in our young learners would be, “That letter isn’t pronounced? Well, it MUST be there for a reason. I wonder what it is? Do you want to help me find out?”

Mrs. Steven's Classroom Blog

It's all about memorable learning

etymology

“I’ll retire to Bedlam”

credit to marfis 75 on flicker

When You Have a Febriferous Illness, You Need a Febrifuge!

fŭgo, fŭgare, fugāvi, fugātum
“to put to flight, drive or chase away”

fŭgĭo, fŭgere, fŭgi, fŭgĭtum
“run away”

Waiting for the Tides to Change

Instead of Being Submerged in a Sea of “Sound It Out”, We Suggest Spelling Success with Structured Word Inquiry!

Having a Blast! Creating a Podcast!

“Button up your overcoat when the wind is free….” Ruth Etting

Conferences: An Opportunity to Get the Word Out

“Outer Beauty Attracts, but Inner Beauty Captivates.” ~Kate Angell

“Stop Learning and Start Thinking”

Guess What? They’re ALL Silent Letters!

credit to marfis 75 on flicker

fŭgo, fŭgare, fugāvi, fugātum “to put to flight, drive or chase away”

fŭgĭo, fŭgere, fŭgi, fŭgĭtum “run away”

fŭgo, fŭgare, fugāvi, fugātum
“to put to flight, drive or chase away”

fŭgĭo, fŭgere, fŭgi, fŭgĭtum
“run away”